Análisis de datos espaciales en R

Manejo de datos espaciales en R

Diego Nieto Lugilde

Universidad de Córdoba (España)

2024-10-15

Introducción a los datos espaciales

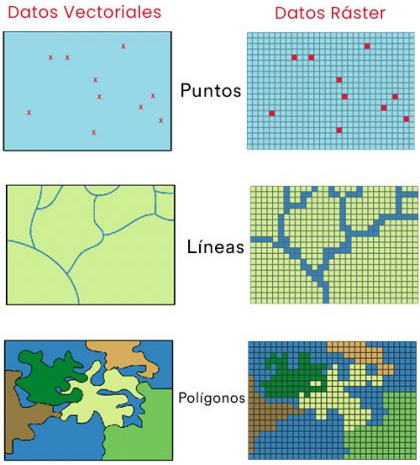
¿Qué son los datos espaciales?

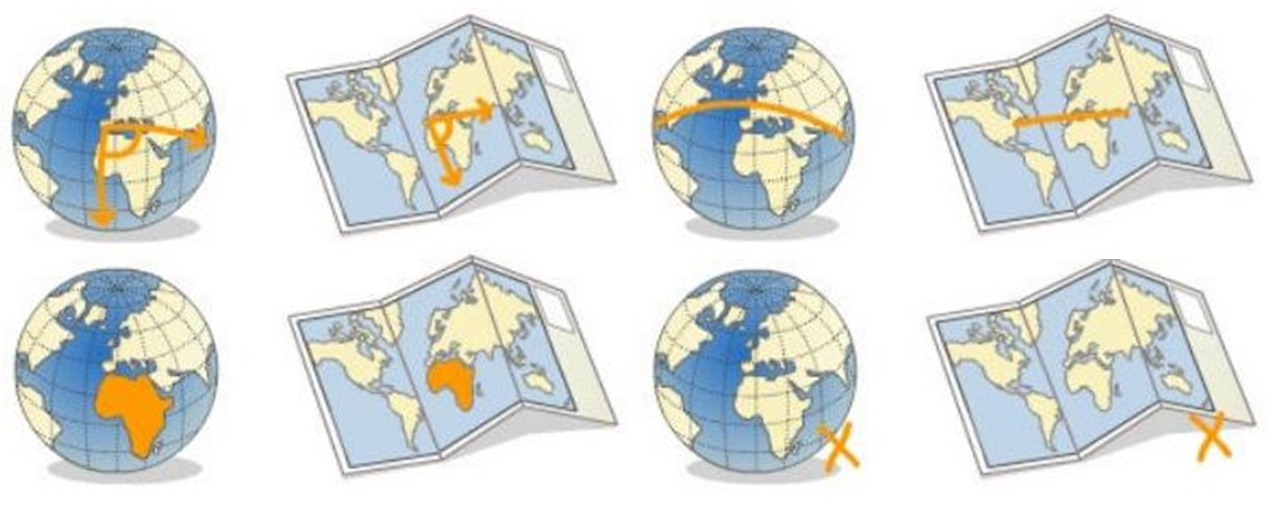
La misma información se puede representar de varias maneras

Algunos tipos de datos se ajustan mejor a ciertas formas de representación

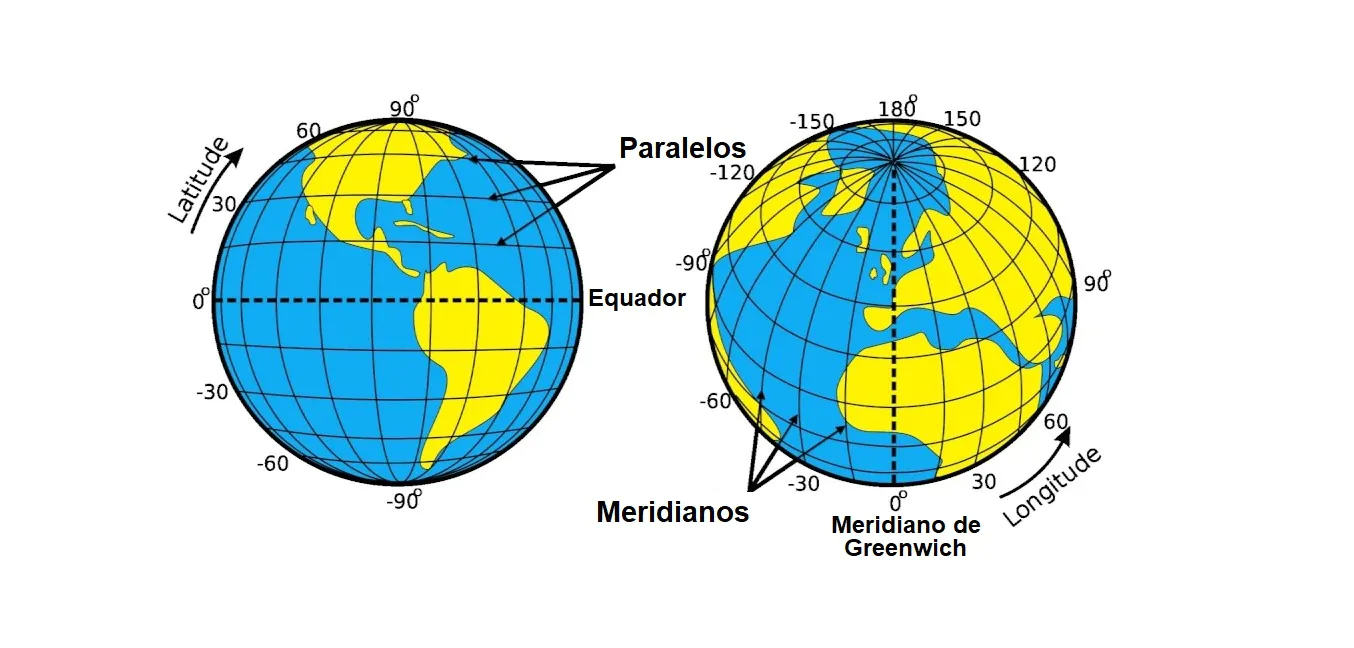
¿Cómo se localiza la información?

No parece fácil medir los ángulos ;)

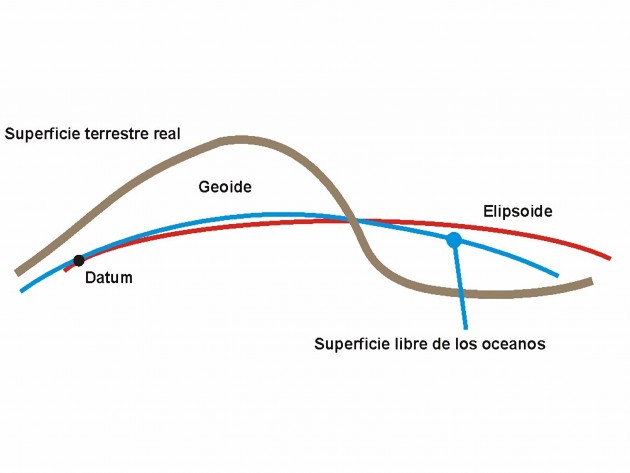
Se calculan aproximaciones usando modelos de la Tierra (Datum)

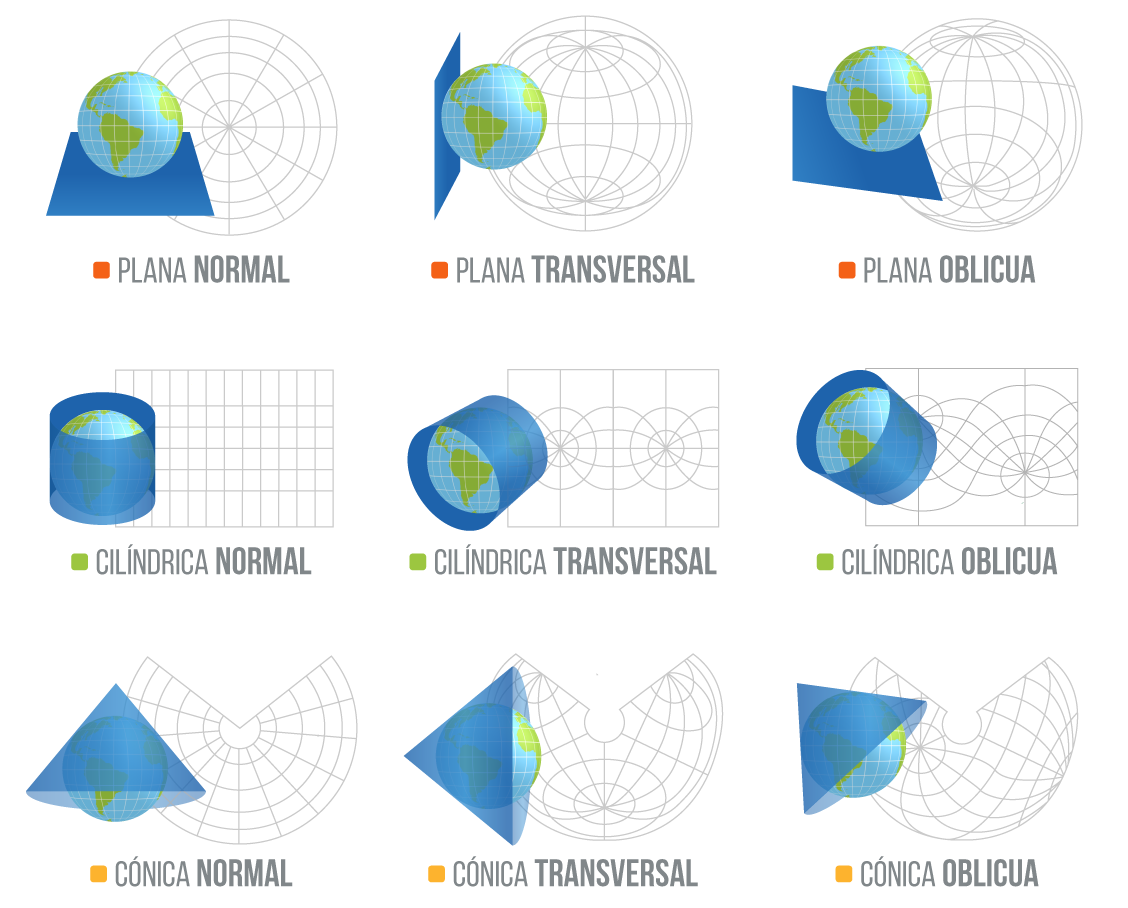
No es lo mismo saber donde ocurre algo que dibujarlo en un mapa

Para ello es necesario proyectar una esfera sobre un plano

Cada proyección y cada datum genera mapas con propiedades diferentes

Conformes, equidistantes, equivalentes y afiláticas

Manejando datos espaciales

Vamos a usar el paquete terra

# install.packages("terra")
library(terra)

Manejando datos vectoriales

Podemos crear datos vectoriales desde cero

Los más sencillos de crear son los puntos

lon <- c(-116.7, -120.4, -116.7, -113.5, -115.5, -120.8, -119.5, -113.7, -113.7, -110.7) 
lat <- c(45.3, 42.6, 38.9, 42.1, 35.7, 38.9, 36.2, 39, 41.6, 36.9) 
lonlat <- cbind(lon, lat) 
pts <- vect(lonlat) 
pts

 class       : SpatVector 
 geometry    : points 
 dimensions  : 10, 0  (geometries, attributes)
 extent      : -120.8, -110.7, 35.7, 45.3  (xmin, xmax, ymin, ymax)
 coord. ref. :  

Warning

Fijaros que el apartado “coord. ref.” está vacío

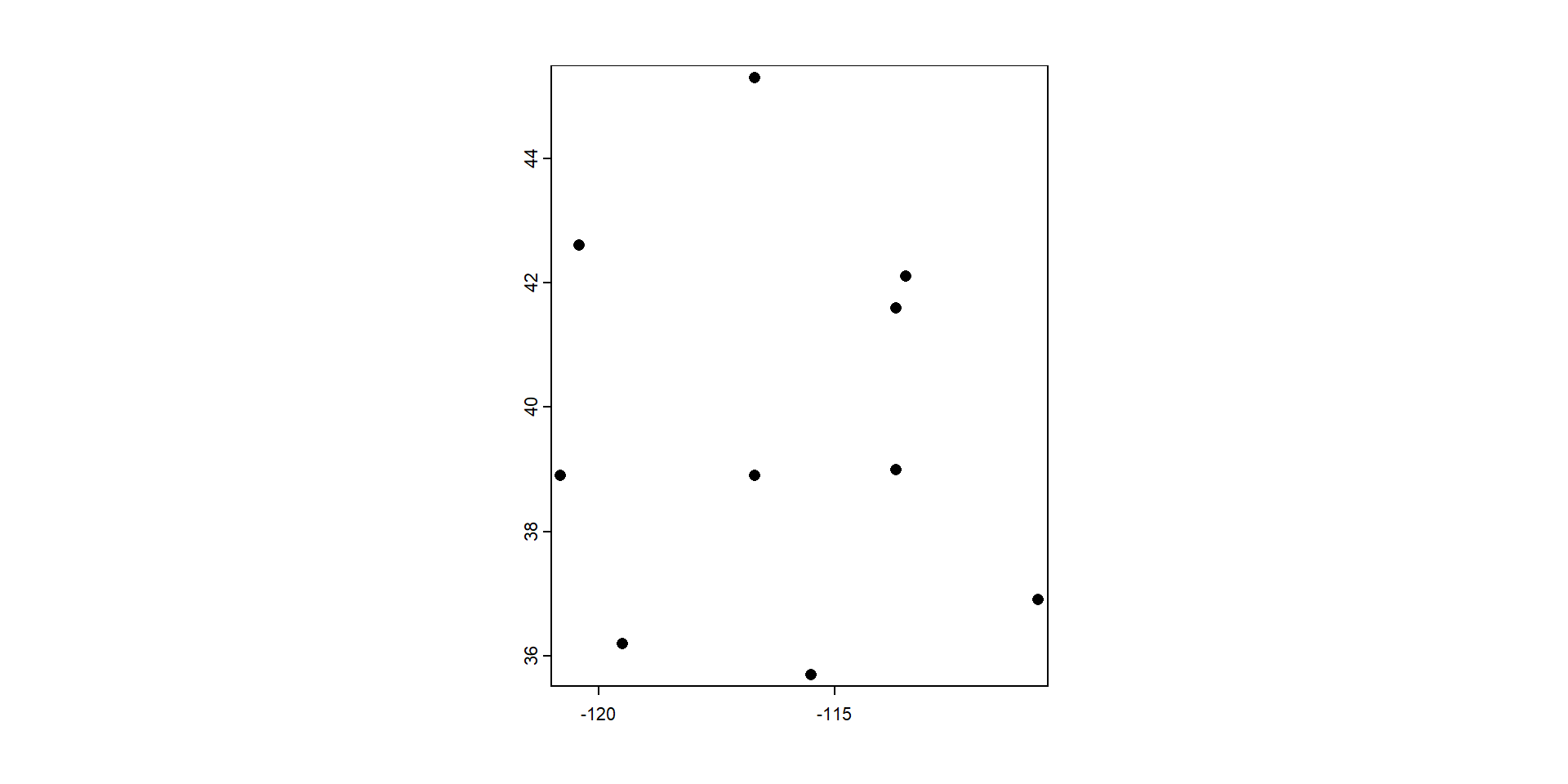
Revisamos el tipo de datos

class(pts)

[1] "SpatVector"
attr(,"package")
[1] "terra"

geom(pts)

      geom part      x    y hole
 [1,]    1    1 -116.7 45.3    0
 [2,]    2    1 -120.4 42.6    0
 [3,]    3    1 -116.7 38.9    0
 [4,]    4    1 -113.5 42.1    0
 [5,]    5    1 -115.5 35.7    0
 [6,]    6    1 -120.8 38.9    0
 [7,]    7    1 -119.5 36.2    0
 [8,]    8    1 -113.7 39.0    0
 [9,]    9    1 -113.7 41.6    0
[10,]   10    1 -110.7 36.9    0

Veamos la distribución espacial de los datos

plot(pts)

Definimos el sistema de referencia de coordenadas (CRS)

crdref <- "+proj=longlat +datum=WGS84"
pts <- vect(lonlat, crs = crdref)
pts

 class       : SpatVector 
 geometry    : points 
 dimensions  : 10, 0  (geometries, attributes)
 extent      : -120.8, -110.7, 35.7, 45.3  (xmin, xmax, ymin, ymax)
 coord. ref. : +proj=longlat +datum=WGS84 +no_defs 

Podemos comprobar el CRS de un objeto vectorial

crs(pts)

[1] "GEOGCRS[\"unknown\",\n    DATUM[\"World Geodetic System 1984\",\n        ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n            LENGTHUNIT[\"metre\",1]],\n        ID[\"EPSG\",6326]],\n    PRIMEM[\"Greenwich\",0,\n        ANGLEUNIT[\"degree\",0.0174532925199433],\n        ID[\"EPSG\",8901]],\n    CS[ellipsoidal,2],\n        AXIS[\"longitude\",east,\n            ORDER[1],\n            ANGLEUNIT[\"degree\",0.0174532925199433,\n                ID[\"EPSG\",9122]]],\n        AXIS[\"latitude\",north,\n            ORDER[2],\n            ANGLEUNIT[\"degree\",0.0174532925199433,\n                ID[\"EPSG\",9122]]]]"

La ubicación sola no es muy interesante…

Voy a simular valores de precipitación al azar (sample), un valor para cada punto

precipvalue <- sample(1:100, 10)
df <- data.frame(ID = 1:nrow(lonlat), 
                 precip = precipvalue)
pts <- vect(lonlat, atts = df, crs = crdref)
pts

 class       : SpatVector 
 geometry    : points 
 dimensions  : 10, 2  (geometries, attributes)
 extent      : -120.8, -110.7, 35.7, 45.3  (xmin, xmax, ymin, ymax)
 coord. ref. : +proj=longlat +datum=WGS84 +no_defs 
 names       :    ID precip
 type        : <int>  <int>
 values      :     1    100
                   2     42
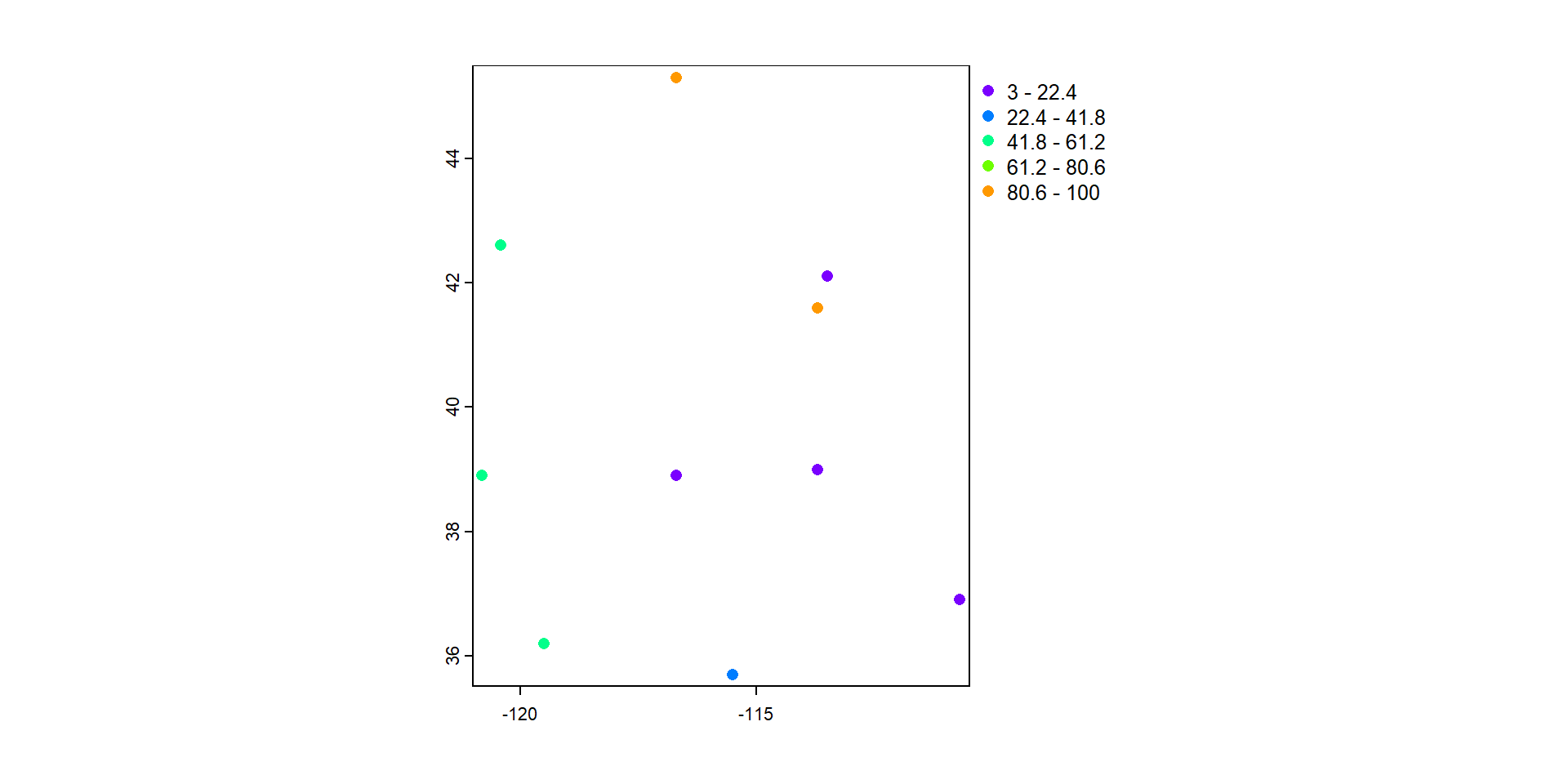
                   3     13

Veamos las precipitaciones en su contexto espacial

plot(pts, "precip", type = "interval")

Vamos a generar ahora un segundo conjunto de puntos…

lon2 <- c(-116.8, -114.2, -112.9, -111.9, -114.2, -115.4, -117.7)
lat2 <- c(41.3, 42.9, 42.4, 39.8, 37.6, 38.3, 37.6)
lonlat2 <- cbind(id = c(1,1,1,1,1,1,1), part = c(1,1,1,1,1,1,1), lon2, lat2)
lonlat2

     id part   lon2 lat2
[1,]  1    1 -116.8 41.3
[2,]  1    1 -114.2 42.9
[3,]  1    1 -112.9 42.4
[4,]  1    1 -111.9 39.8
[5,]  1    1 -114.2 37.6
[6,]  1    1 -115.4 38.3
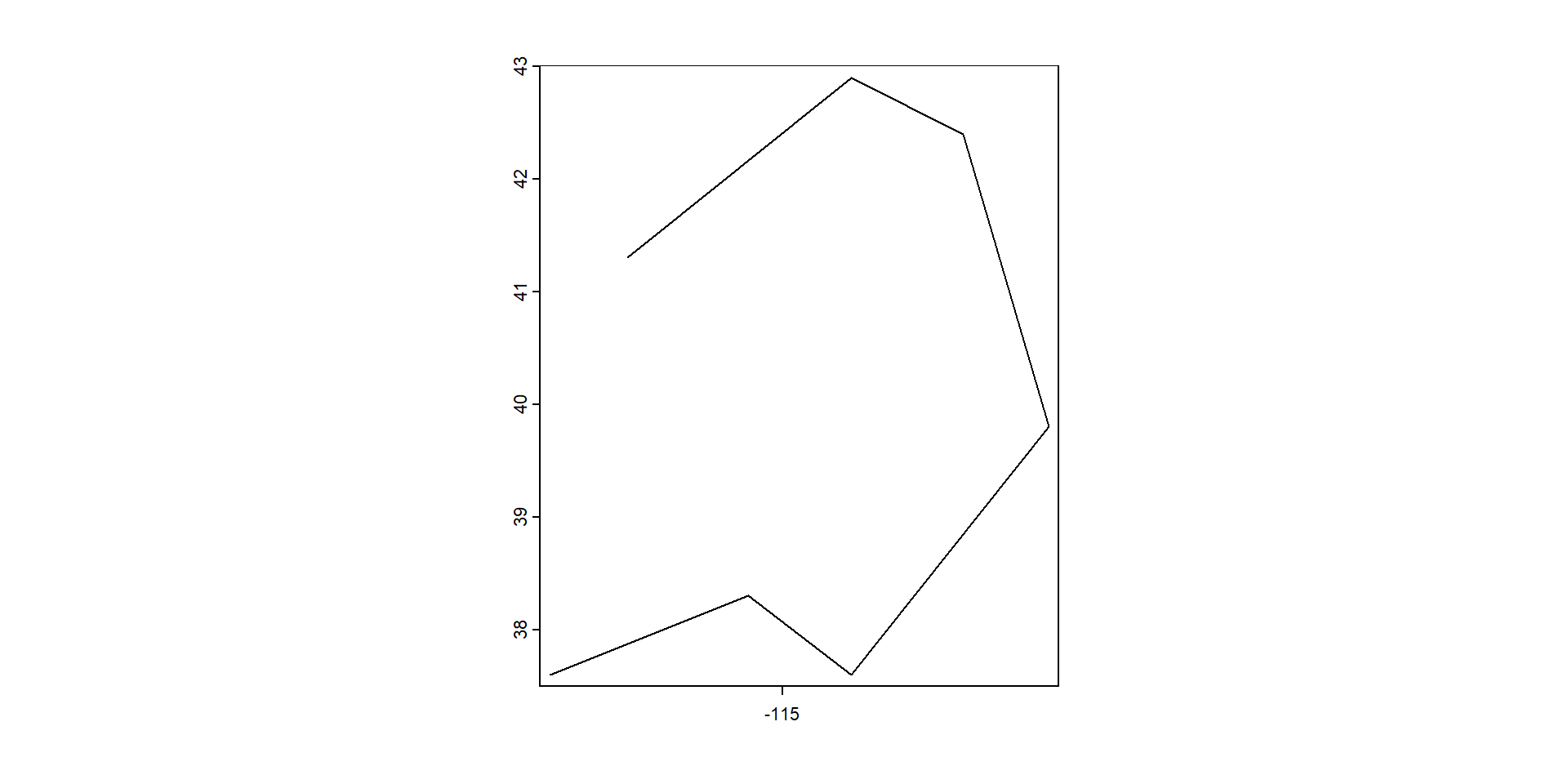
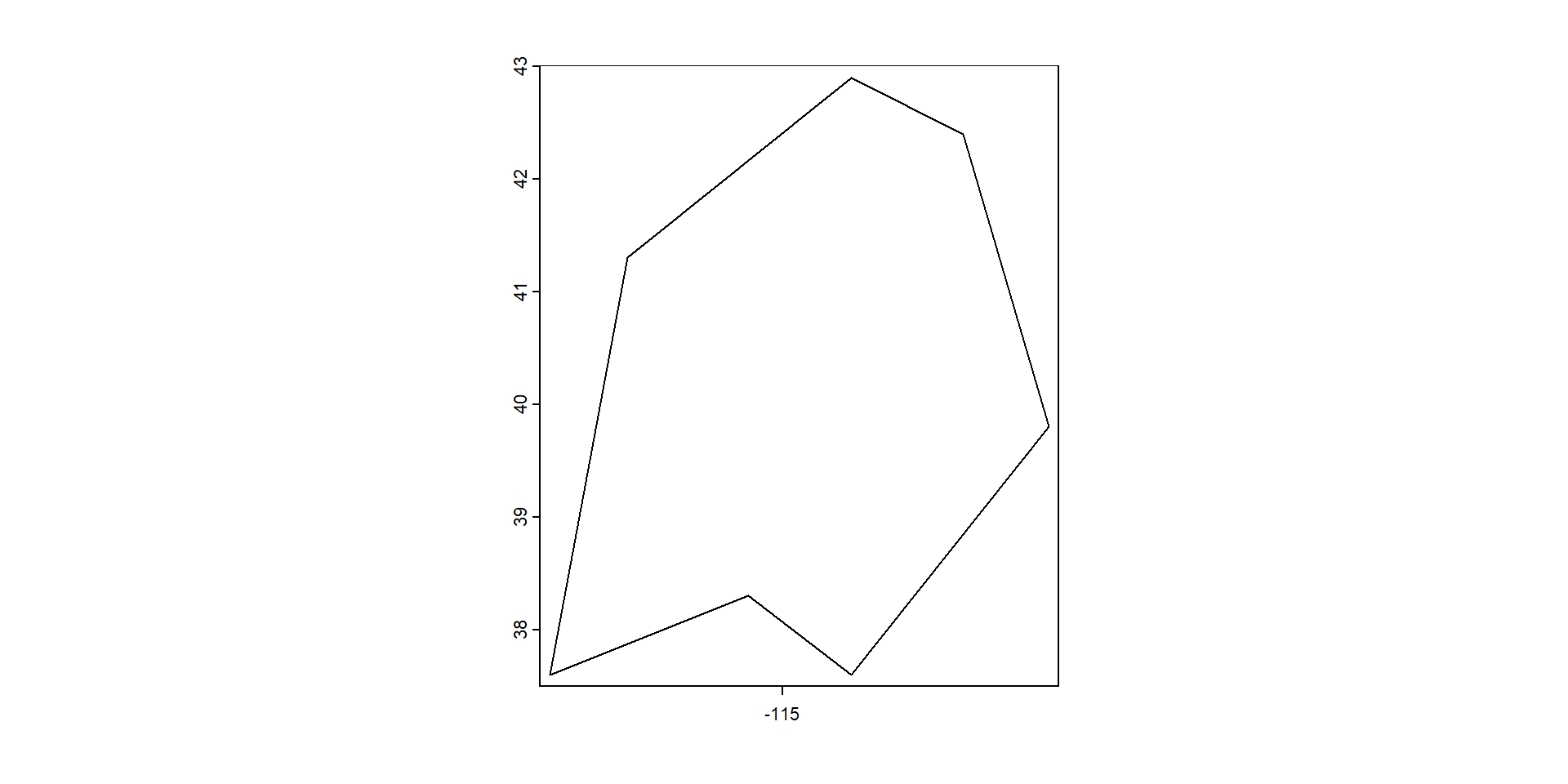
[7,]  1    1 -117.7 37.6

… pero para crear datos de líneas…

lns <- vect(lonlat2, type = "lines", crs = crdref)
lns

 class       : SpatVector 
 geometry    : lines 
 dimensions  : 1, 0  (geometries, attributes)
 extent      : -117.7, -111.9, 37.6, 42.9  (xmin, xmax, ymin, ymax)
 coord. ref. : +proj=longlat +datum=WGS84 +no_defs 

plot(lns)

… o un datos de polígonos

pols <- vect(lonlat2, type = "polygons", crs = crdref)
pols

 class       : SpatVector 
 geometry    : polygons 
 dimensions  : 1, 0  (geometries, attributes)
 extent      : -117.7, -111.9, 37.6, 42.9  (xmin, xmax, ymin, ymax)
 coord. ref. : +proj=longlat +datum=WGS84 +no_defs 

plot(pols)

Lo más normal es usar datos generados con un SIG

Descargar datos de Internet (v.gr. GADM) y cargarlos desde el disco duro

arg <- vect("gadm/gadm41_ARG_1.shp")
arg

Lo más normal es usar datos generados con un SIG

Hay paquetes de R que dan acceso directo a datos vectoriales (v.gr. geodata)

# install.packages("geodata")
library(geodata)
arg <- gadm("ARG", level = 1, path = ".")
arg

 class       : SpatVector 
 geometry    : polygons 
 dimensions  : 24, 11  (geometries, attributes)
 extent      : -73.56056, -53.59184, -55.06153, -21.78137  (xmin, xmax, ymin, ymax)
 coord. ref. : lon/lat WGS 84 (EPSG:4326) 
 names       :   GID_1 GID_0   COUNTRY       NAME_1       VARNAME_1 NL_NAME_1
 type        :   <chr> <chr>     <chr>        <chr>           <chr>     <chr>
 values      : ARG.1_1   ARG Argentina Buenos Aires Baires|Buenos ~        NA
               ARG.2_1   ARG Argentina    Catamarca              NA        NA
               ARG.3_1   ARG Argentina        Chaco El Chaco|Presi~        NA
    TYPE_1 ENGTYPE_1  CC_1 HASC_1 ISO_1
     <chr>     <chr> <chr>  <chr> <chr>
 Provincia  Province    NA  AR.BA  AR-B
 Provincia  Province    NA  AR.CT  AR-K
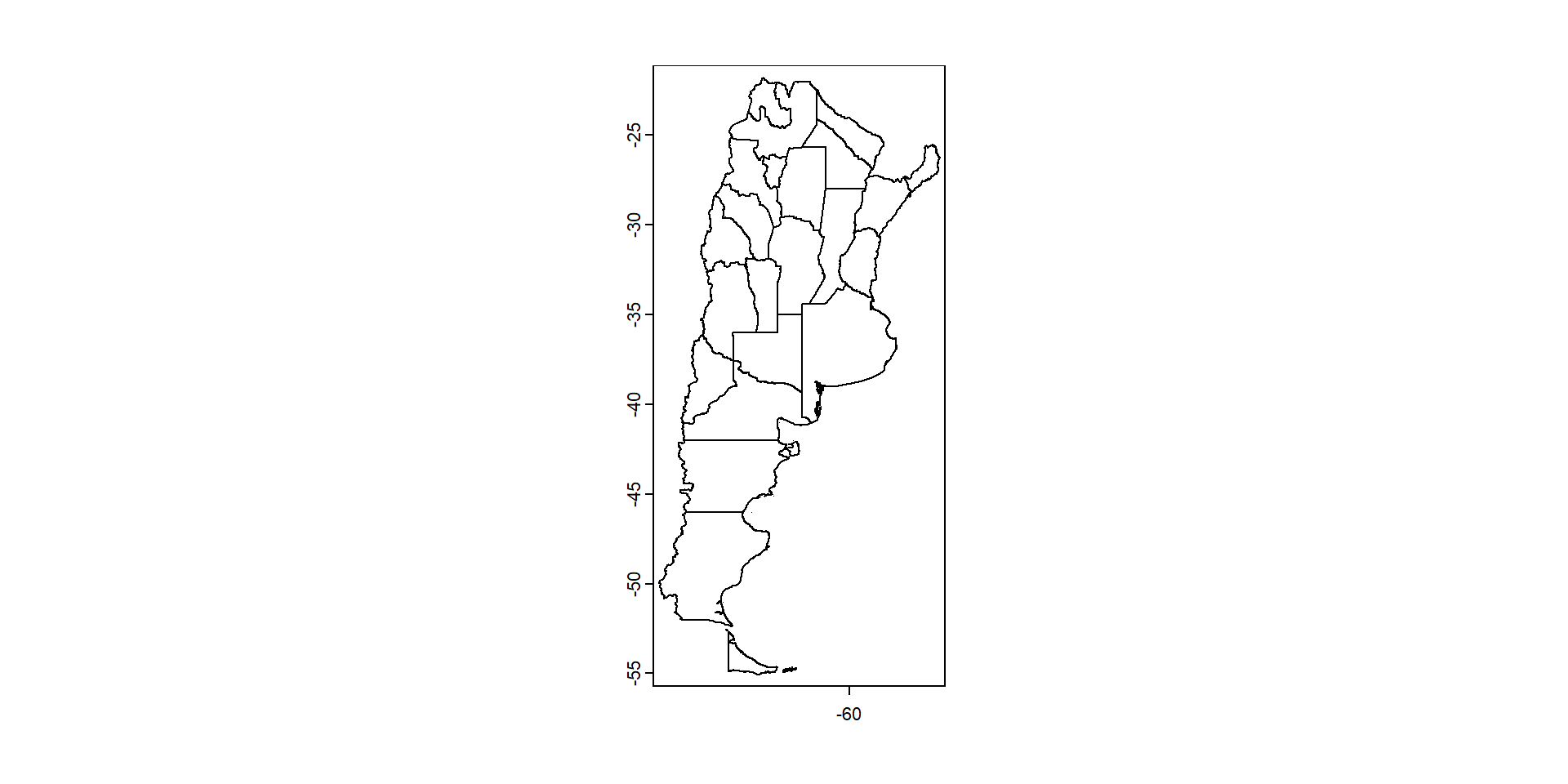
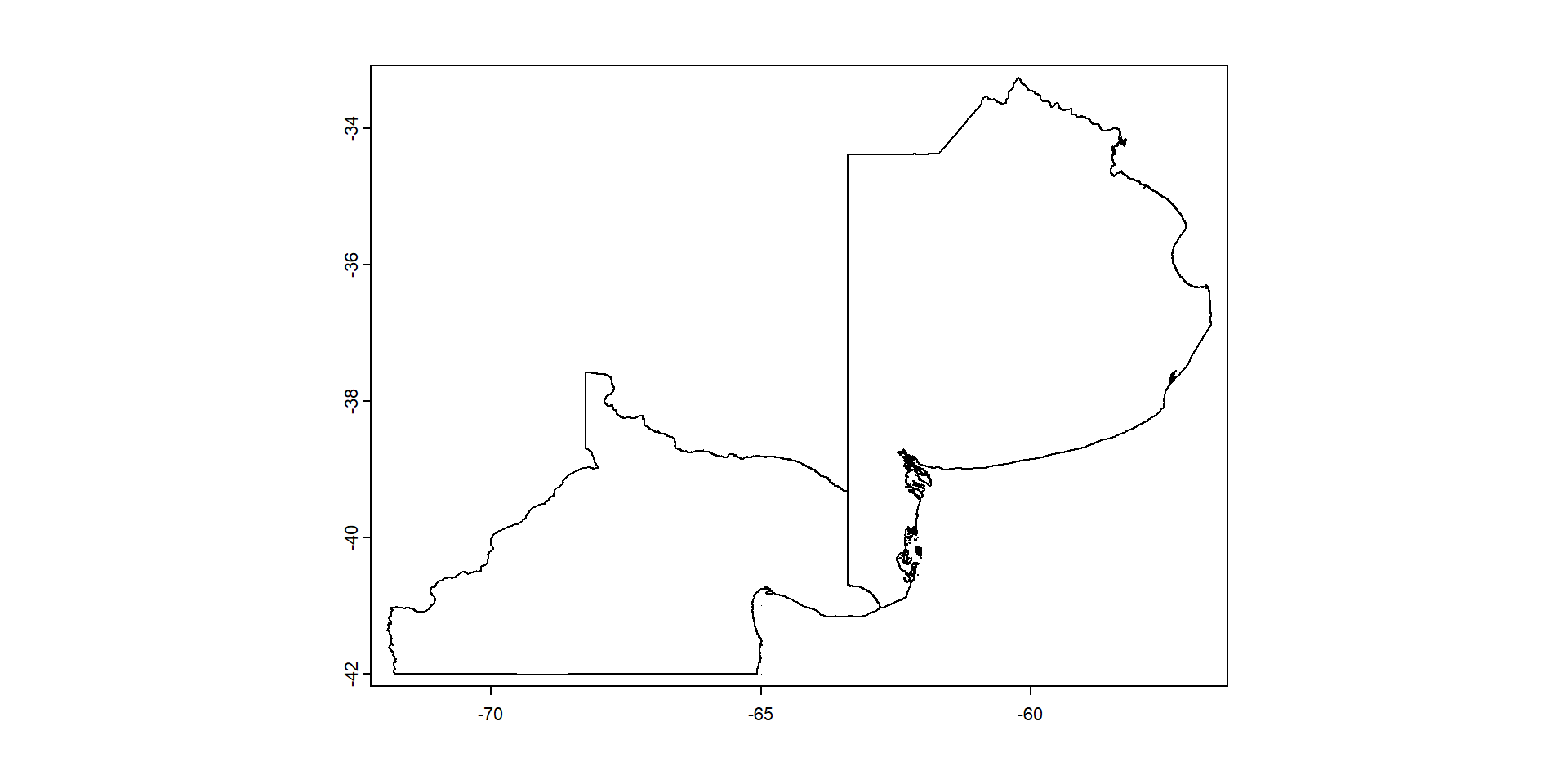
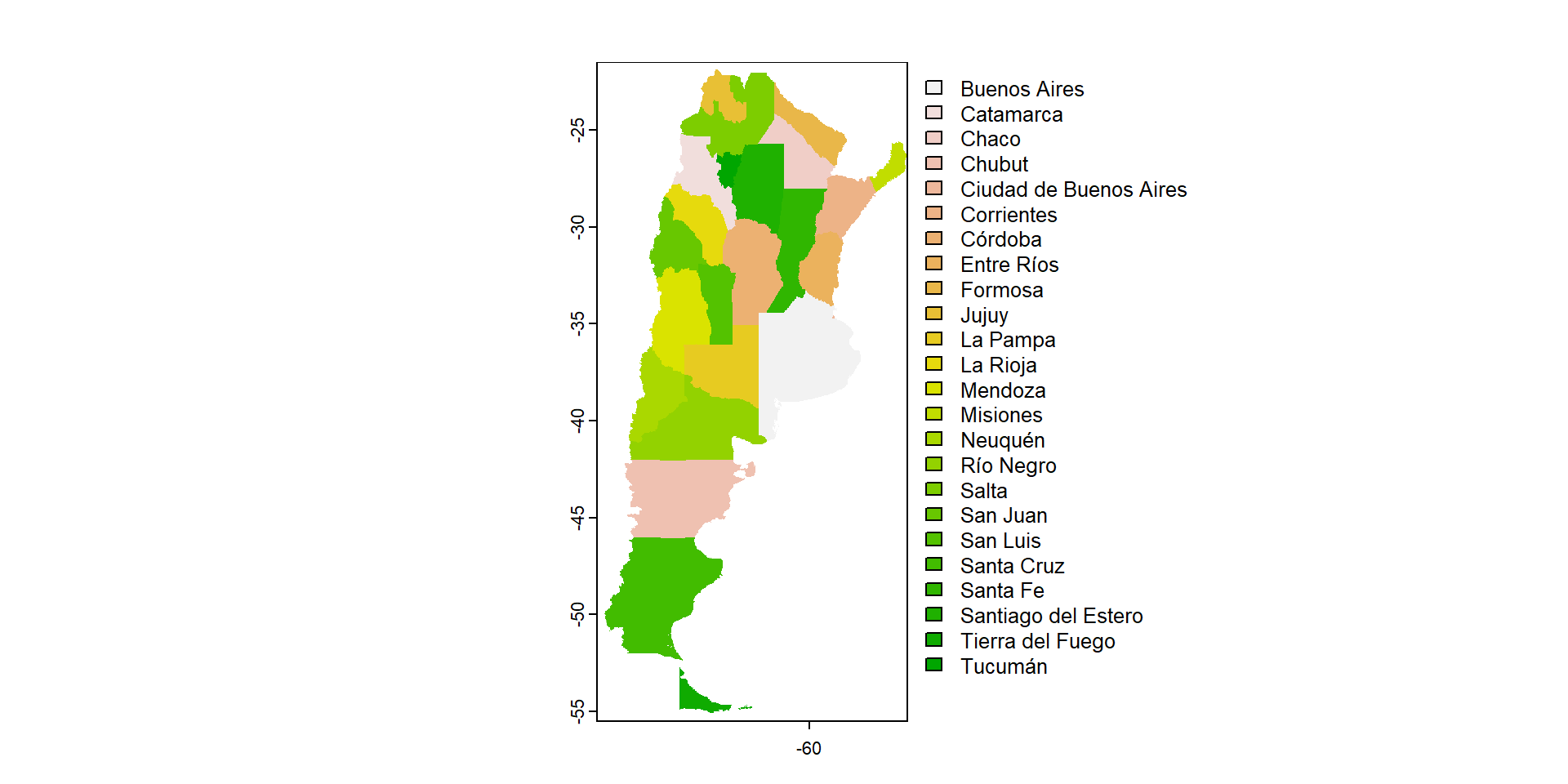
 Provincia  Province    NA  AR.CC  AR-H

Veamos si se parece a lo que conocemos…

plot(arg)

Estos datos se pueden guardar para no tener que volver a descargarlos

writeVector(arg, "arg.shp", overwrite = TRUE)

Comprobemos el CRS de alguno de nuestros datos

crs(arg)

[1] "GEOGCRS[\"WGS 84\",\n    DATUM[\"World Geodetic System 1984\",\n        ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n            LENGTHUNIT[\"metre\",1]]],\n    PRIMEM[\"Greenwich\",0,\n        ANGLEUNIT[\"degree\",0.0174532925199433]],\n    CS[ellipsoidal,2],\n        AXIS[\"geodetic latitude (Lat)\",north,\n            ORDER[1],\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n        AXIS[\"geodetic longitude (Lon)\",east,\n            ORDER[2],\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n    ID[\"EPSG\",4326]]"

Se puede borrar el CRS del conjunto de datos

arg_sin_crs <- arg
crs(arg_sin_crs) <- ""
crs(arg_sin_crs)

[1] ""

O se puede especificar a mano (estandar PROJ.4)

arg_falso_utm <- arg
crs(arg_falso_utm) <- "+proj=utm +zone=19 +south +datum=WGS84 +units=m +no_defs +type=crs"
crs(arg_falso_utm)

[1] "PROJCRS[\"unknown\",\n    BASEGEOGCRS[\"unknown\",\n        DATUM[\"World Geodetic System 1984\",\n            ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n                LENGTHUNIT[\"metre\",1]],\n            ID[\"EPSG\",6326]],\n        PRIMEM[\"Greenwich\",0,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8901]]],\n    CONVERSION[\"UTM zone 19S\",\n        METHOD[\"Transverse Mercator\",\n            ID[\"EPSG\",9807]],\n        PARAMETER[\"Latitude of natural origin\",0,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8801]],\n        PARAMETER[\"Longitude of natural origin\",-69,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8802]],\n        PARAMETER[\"Scale factor at natural origin\",0.9996,\n            SCALEUNIT[\"unity\",1],\n            ID[\"EPSG\",8805]],\n        PARAMETER[\"False easting\",500000,\n            LENGTHUNIT[\"metre\",1],\n            ID[\"EPSG\",8806]],\n        PARAMETER[\"False northing\",10000000,\n            LENGTHUNIT[\"metre\",1],\n            ID[\"EPSG\",8807]],\n        ID[\"EPSG\",17019]],\n    CS[Cartesian,2],\n        AXIS[\"(E)\",east,\n            ORDER[1],\n            LENGTHUNIT[\"metre\",1,\n                ID[\"EPSG\",9001]]],\n        AXIS[\"(N)\",north,\n            ORDER[2],\n            LENGTHUNIT[\"metre\",1,\n                ID[\"EPSG\",9001]]]]"

O se puede especificar con los códigos EPSG

arg_false_utm2 <- arg
crs(arg_false_utm2) <- "EPSG:32719"
crs(arg_false_utm2)

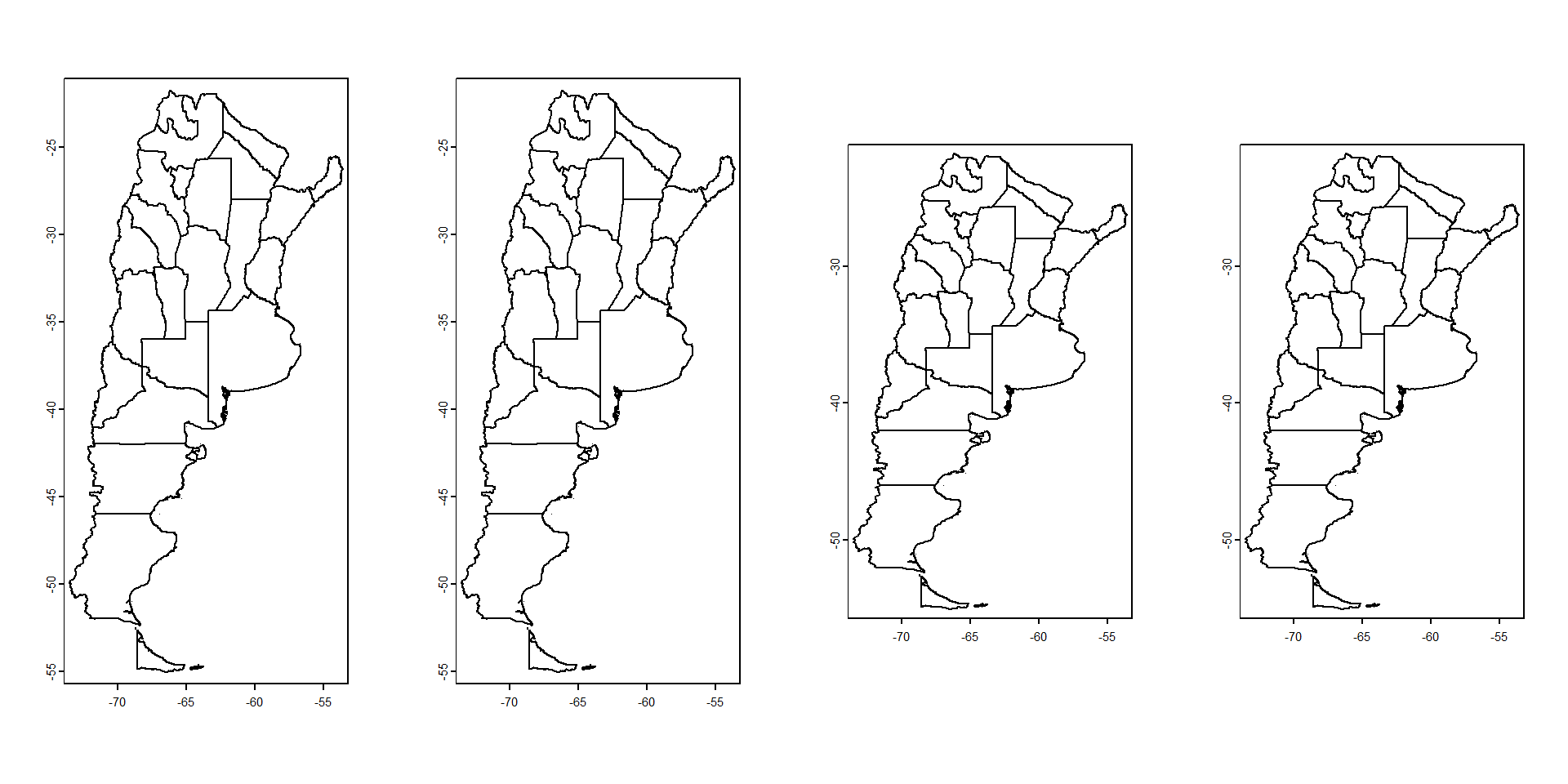
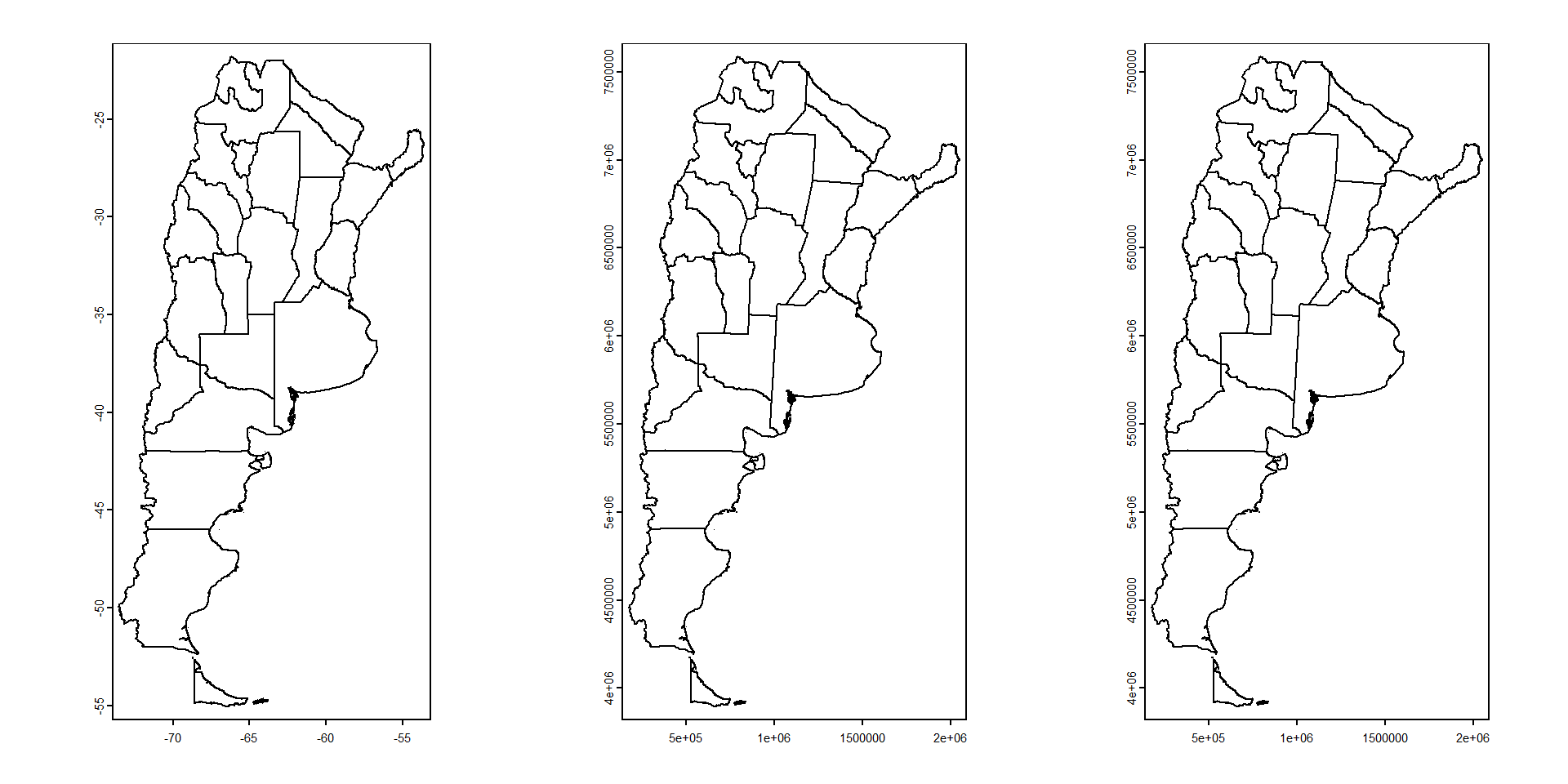
[1] "PROJCRS[\"WGS 84 / UTM zone 19S\",\n    BASEGEOGCRS[\"WGS 84\",\n        ENSEMBLE[\"World Geodetic System 1984 ensemble\",\n            MEMBER[\"World Geodetic System 1984 (Transit)\"],\n            MEMBER[\"World Geodetic System 1984 (G730)\"],\n            MEMBER[\"World Geodetic System 1984 (G873)\"],\n            MEMBER[\"World Geodetic System 1984 (G1150)\"],\n            MEMBER[\"World Geodetic System 1984 (G1674)\"],\n            MEMBER[\"World Geodetic System 1984 (G1762)\"],\n            MEMBER[\"World Geodetic System 1984 (G2139)\"],\n            ELLIPSOID[\"WGS 84\",6378137,298.257223563,\n                LENGTHUNIT[\"metre\",1]],\n            ENSEMBLEACCURACY[2.0]],\n        PRIMEM[\"Greenwich\",0,\n            ANGLEUNIT[\"degree\",0.0174532925199433]],\n        ID[\"EPSG\",4326]],\n    CONVERSION[\"UTM zone 19S\",\n        METHOD[\"Transverse Mercator\",\n            ID[\"EPSG\",9807]],\n        PARAMETER[\"Latitude of natural origin\",0,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8801]],\n        PARAMETER[\"Longitude of natural origin\",-69,\n            ANGLEUNIT[\"degree\",0.0174532925199433],\n            ID[\"EPSG\",8802]],\n        PARAMETER[\"Scale factor at natural origin\",0.9996,\n            SCALEUNIT[\"unity\",1],\n            ID[\"EPSG\",8805]],\n        PARAMETER[\"False easting\",500000,\n            LENGTHUNIT[\"metre\",1],\n            ID[\"EPSG\",8806]],\n        PARAMETER[\"False northing\",10000000,\n            LENGTHUNIT[\"metre\",1],\n            ID[\"EPSG\",8807]]],\n    CS[Cartesian,2],\n        AXIS[\"(E)\",east,\n            ORDER[1],\n            LENGTHUNIT[\"metre\",1]],\n        AXIS[\"(N)\",north,\n            ORDER[2],\n            LENGTHUNIT[\"metre\",1]],\n    USAGE[\n        SCOPE[\"Navigation and medium accuracy spatial referencing.\"],\n        AREA[\"Between 72°W and 66°W, southern hemisphere between 80°S and equator, onshore and offshore. Argentina. Bolivia. Brazil. Chile. Colombia. Peru.\"],\n        BBOX[-80,-72,0,-66]],\n    ID[\"EPSG\",32719]]"

Cambia el CRS pero no las coordenadas en si

par(mfrow = c(1, 4))
plot(arg)
plot(arg_sin_crs)
plot(arg_falso_utm)
plot(arg_false_utm2)

Note

Cambia la representación gráfica porque las unidades cambian entre CRS (grados o metros). Mientras los metros se representan igual en el eje horizontal y vertical, los grados geográficos no.

Para convertir coordenadas entre diferentes CRSs tenemos que proyectar los datos

arg_utm19s <- project(arg, "+proj=utm +zone=19 +south +datum=WGS84 +units=m +no_defs +type=crs")
arg_4326 <- project(arg, "EPSG:32719")
par(mfrow = c(1, 3))
plot(arg)
plot(arg_utm19s)
plot(arg_4326)

También se puede filtrar la información para una o varias entidades de los datos

which(arg$NAME_1 == "Buenos Aires")

[1] 1

i <- which(arg$NAME_1 %in% c("Buenos Aires", "Río Negro"))
g <- arg[i,]
plot(g)

Momento para practicar

Ejercicios de clase

Parte 1: Trabajando con datos vectoriales

Manejando datos ráster

Podemos crear datos ráster desde cero

r <- rast(ncol = 10, nrow = 10, 
          xmin = -150, xmax = -80, 
          ymin = 20, ymax = 60)
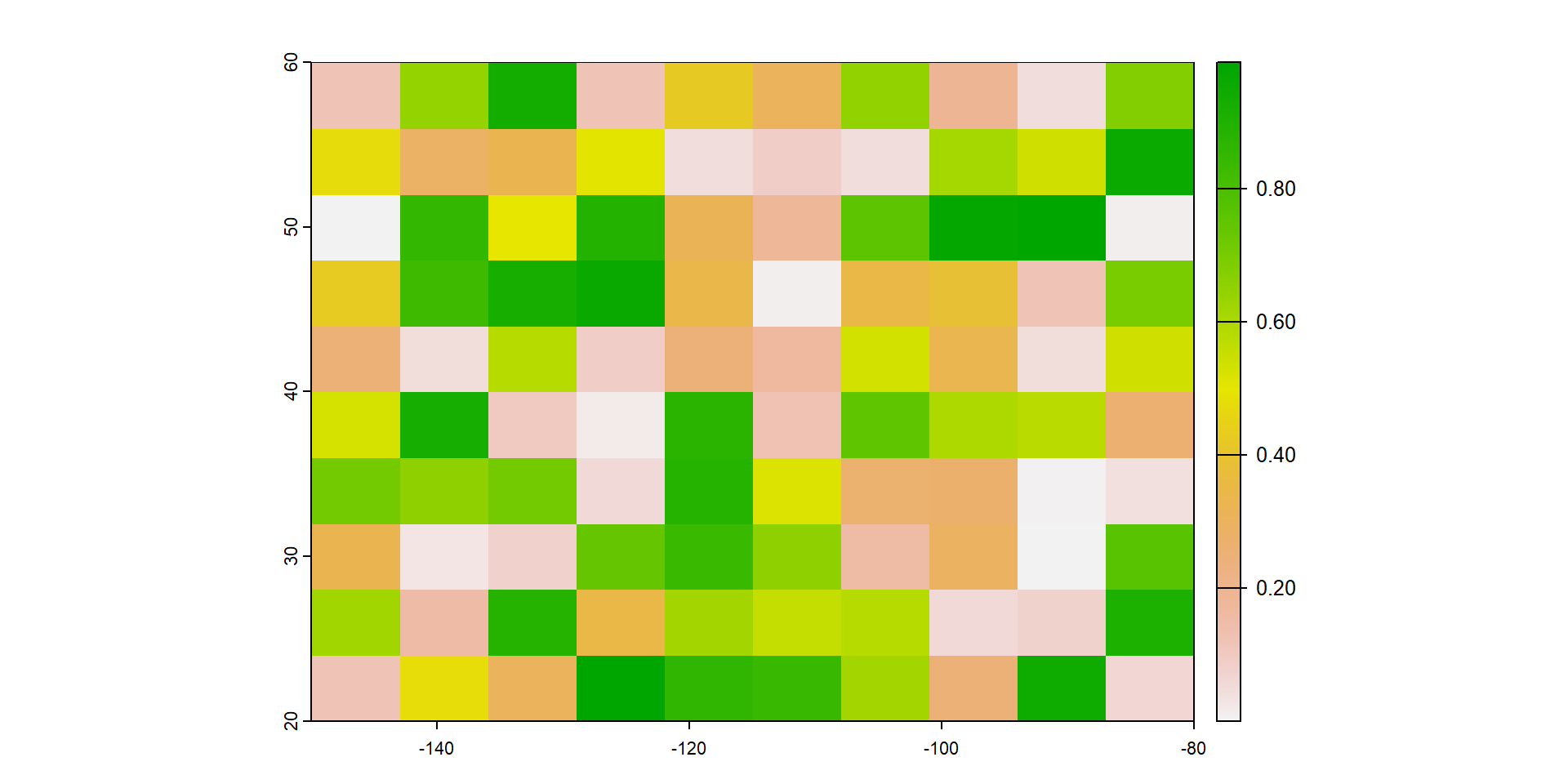
values(r) <- runif(ncell(r))
r

class       : SpatRaster 
dimensions  : 10, 10, 1  (nrow, ncol, nlyr)
resolution  : 7, 4  (x, y)
extent      : -150, -80, 20, 60  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (CRS84) (OGC:CRS84) 
source(s)   : memory
name        :        lyr.1 
min value   : 0.0007290391 
max value   : 0.9898839085 

Veamos que aspecto tienen

plot(r)

Podemos operar con los datos ráster

r2 <- r * r
r3  <- sqrt(r)

Important

Al operar con datos ráster, las operaciones se aplican sobre cada píxel individualmente. Por ello, sólo se pueden realizar operaciones con ráster que tienen el mismo área y el mismo tamaño de píxel. El resultado, por tanto, es un nuevo objeto ráster con las mismas características geográficas, pero cuyos píxeles tienen los valores resultantes de aplicar las funciones matemáticas.

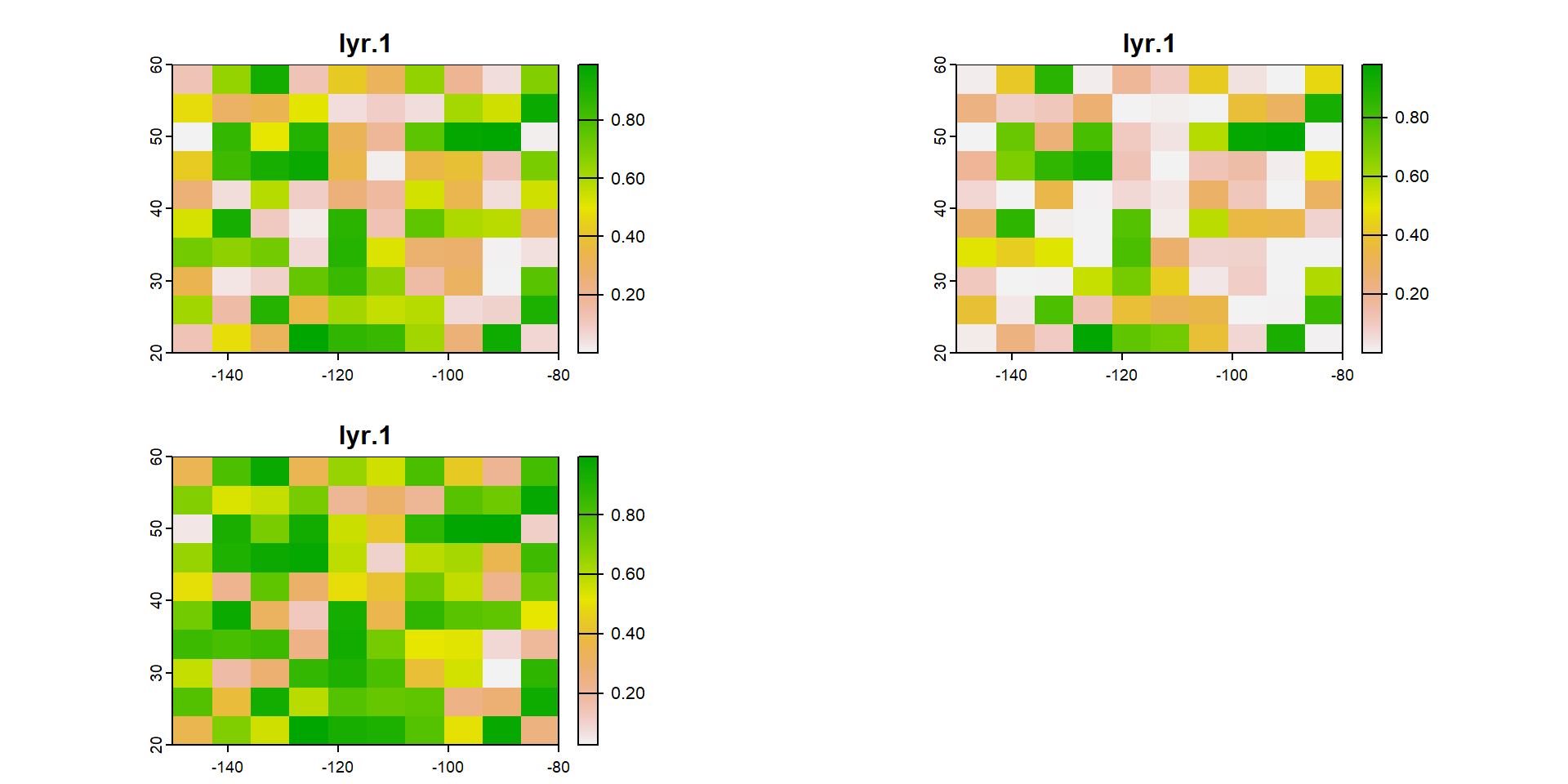
Si trabajamos con muchas capas, mejor crear un objeto multicapa

stck <- c(r, r2, r3)
stck

class       : SpatRaster 
dimensions  : 10, 10, 3  (nrow, ncol, nlyr)
resolution  : 7, 4  (x, y)
extent      : -150, -80, 20, 60  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (CRS84) (OGC:CRS84) 
source(s)   : memory
names       :        lyr.1,        lyr.1,      lyr.1 
min values  : 0.0007290391, 5.314980e-07, 0.02700072 
max values  : 0.9898839085, 9.798702e-01, 0.99492910 

Veamos que aspecto tiene el objeto multicapa

plot(stck)

También se pueden extraer capas de objetos multicapa

r2 <- stck[[2]]
r2

class       : SpatRaster 
dimensions  : 10, 10, 1  (nrow, ncol, nlyr)
resolution  : 7, 4  (x, y)
extent      : -150, -80, 20, 60  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (CRS84) (OGC:CRS84) 
source(s)   : memory
name        :        lyr.1 
min value   : 5.314980e-07 
max value   : 9.798702e-01 

Como antes, lo normal es cargar datos generados en SIG

Para ello podemos descargar datos de distintas fuentes (v.gr. WorldClim)

tavg <- rast("tavg_arg.tif")
tavg

class       : SpatRaster 
dimensions  : 4080, 2460, 12  (nrow, ncol, nlyr)
resolution  : 0.008333333, 0.008333333  (x, y)
extent      : -74, -53.5, -55.5, -21.5  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (EPSG:4326) 
source      : tavg_arg.tif 
names       : ARG_w~avg_1, ARG_w~avg_2, ARG_w~avg_3, ARG_w~avg_4, ARG_w~avg_5, ARG_w~avg_6, ... 
min values  :       -11.1,       -11.8,       -12.5,       -14.5,       -16.7,       -19.8, ... 
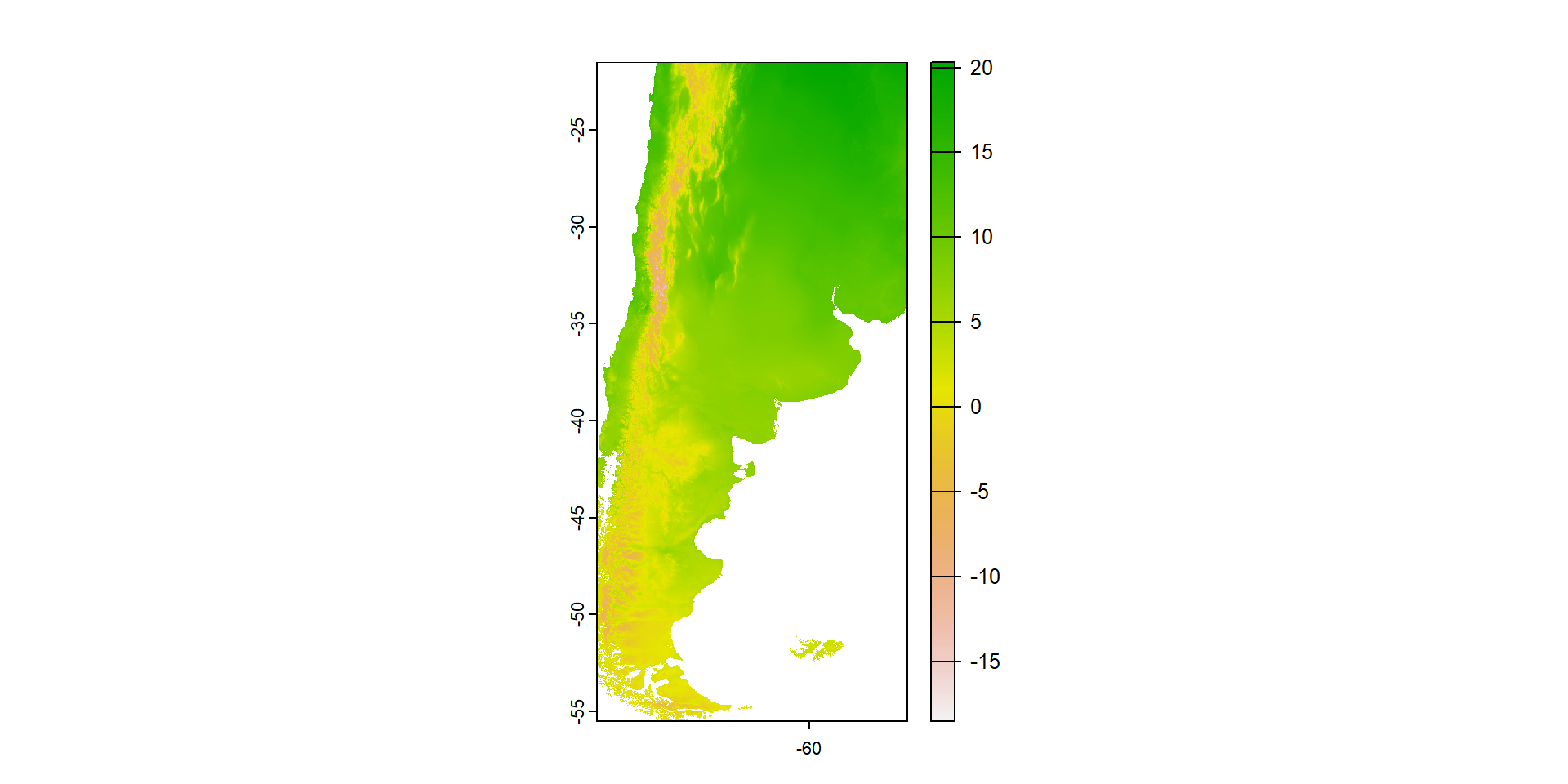
max values  :        29.2,        28.4,        27.3,        25.0,        22.2,        21.0, ... 

Como antes, lo normal es cargar datos generados en SIG

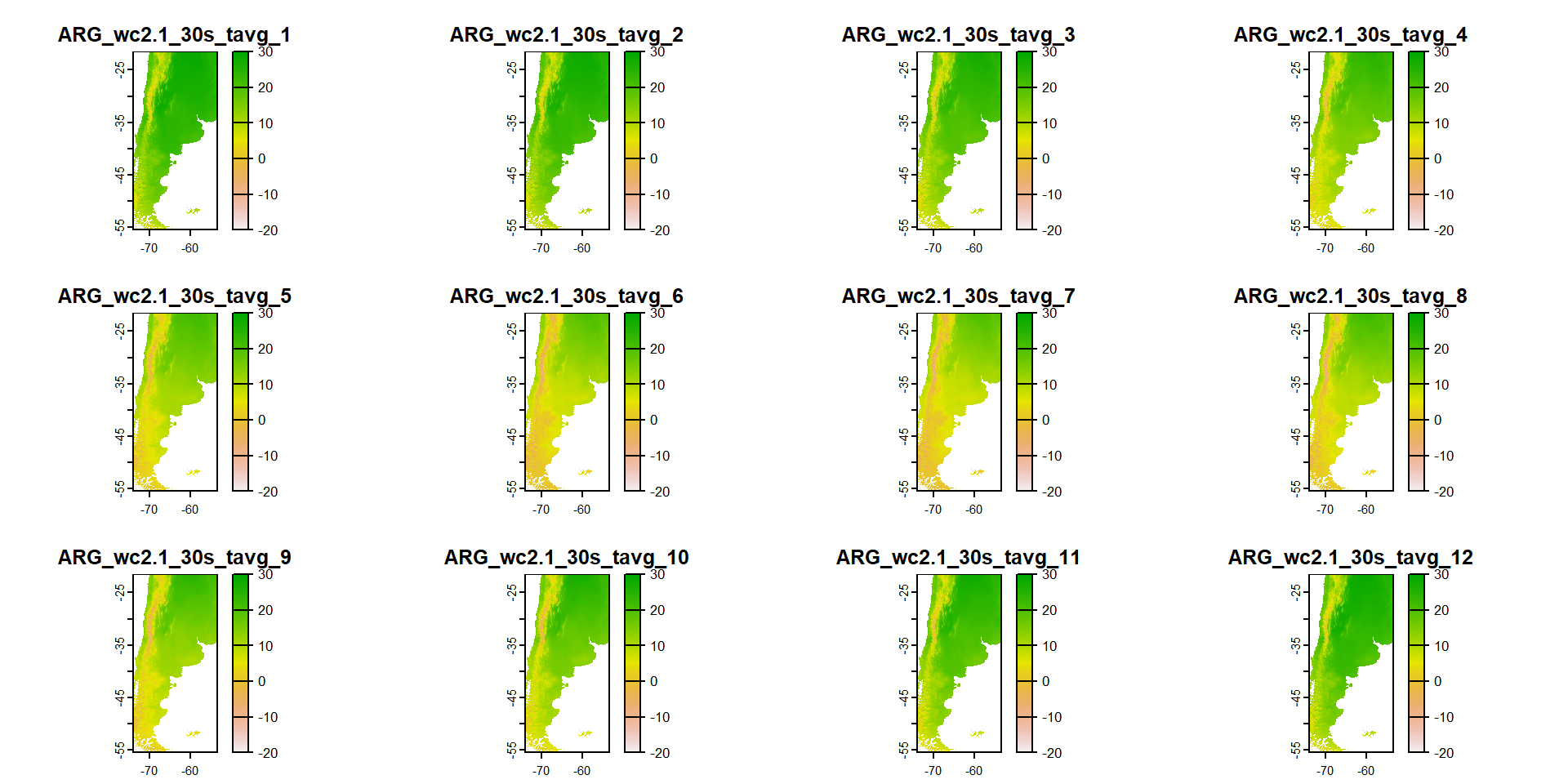
… o podemos usar el paquete geodata para acceder directamente a esa información

tavg <- worldclim_country("ARG", "tavg", path = ".")
tavg

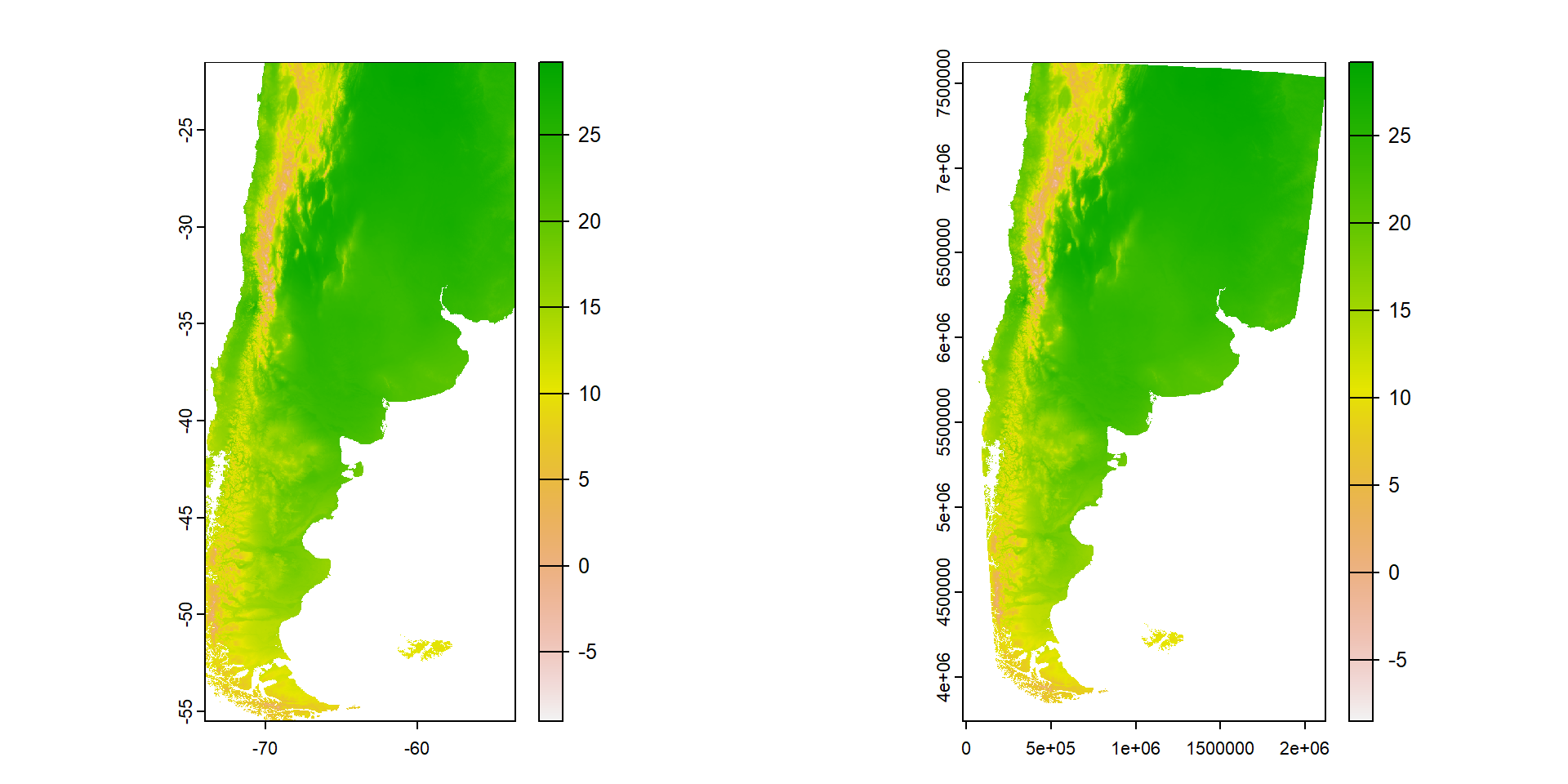
Veamos si se parece a lo que conocemos…

plot(tavg, range = c(-20, 30))

También podemos guardar estos datos para no tener que volver a descargarlos

writeRaster(tavg, "raster_tavg_arg.tif", overwrite = TRUE)

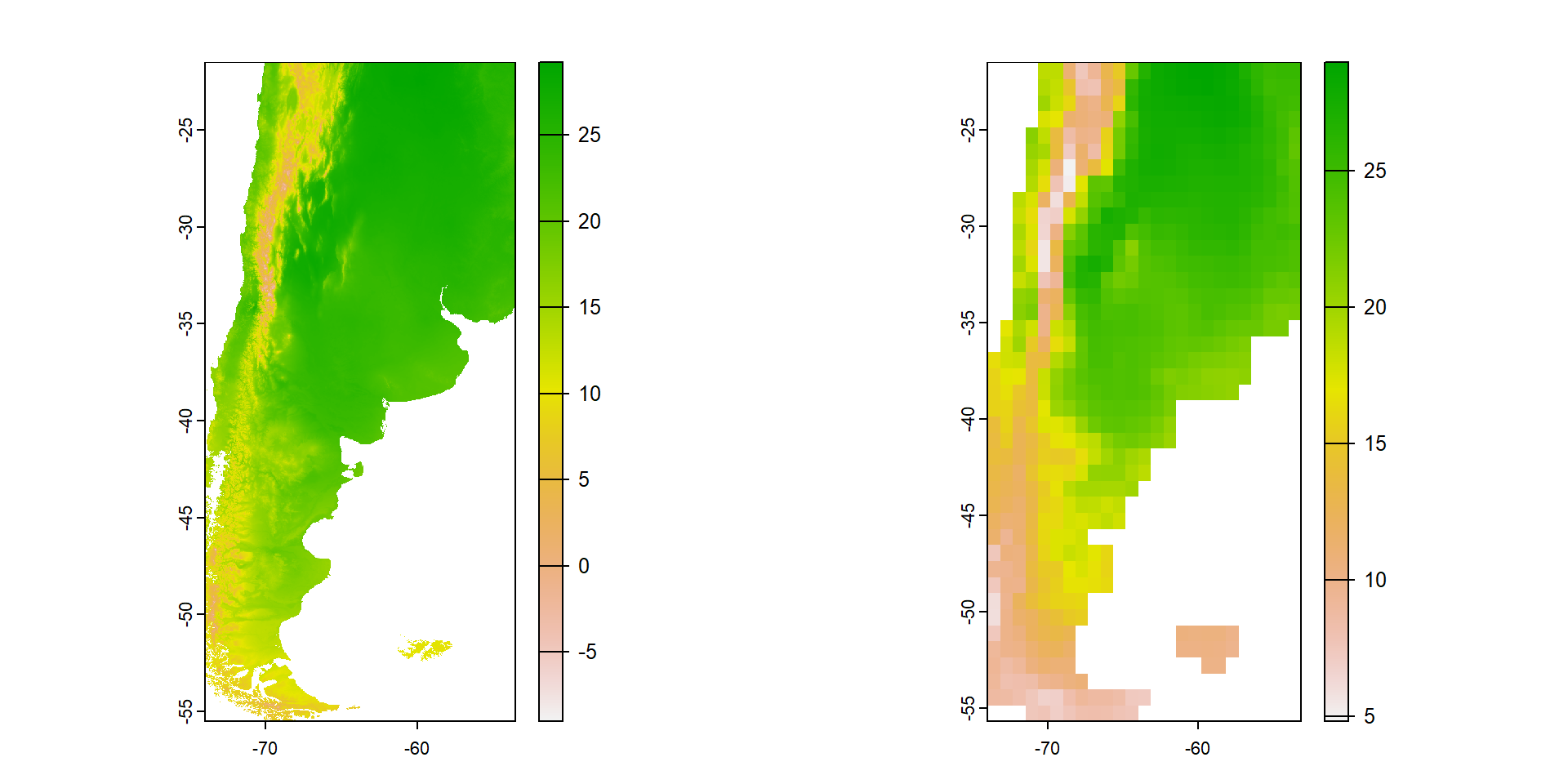
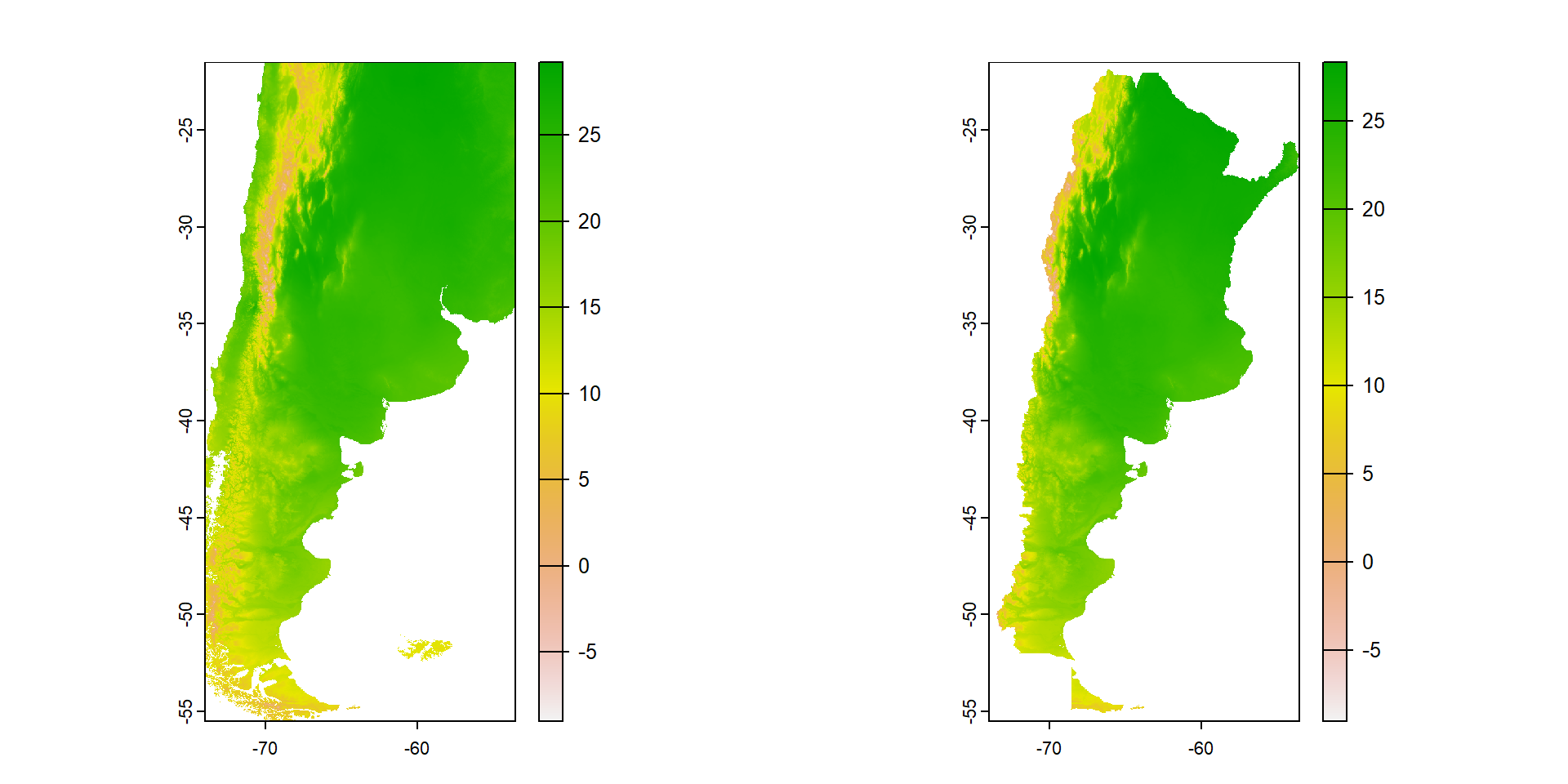
Los datos ráster también se pueden proyectar

tavg_utm19s <- project(tavg, "EPSG:32719")

|---------|---------|---------|---------|
=========================================
                                          

tavg_utm19s

class       : SpatRaster 
dimensions  : 4455, 2454, 12  (nrow, ncol, nlyr)
resolution  : 871.5251, 871.5251  (x, y)
extent      : -18378.29, 2120344, 3739870, 7622514  (xmin, xmax, ymin, ymax)
coord. ref. : WGS 84 / UTM zone 19S (EPSG:32719) 
source      : spat_6a785b9239a_27256.tif 
names       : ARG_w~avg_1, ARG_w~avg_2, ARG_w~avg_3, ARG_w~avg_4, ARG_w~avg_5, ARG_w~avg_6, ... 
min values  :    -10.0618,   -10.72299,   -11.48637,   -13.54974,   -15.83332,   -19.14314, ... 
max values  :     29.2000,    28.40000,    27.30000,    25.00000,    22.20000,    20.97644, ... 

Ahora las coordenadas si aparecen “desplazadas”

par(mfrow = c(1, 2))
plot(tavg[[1]])
plot(tavg_utm19s[[1]])

Warning

No hay una correspondencia exacta de píxeles. Lo veréis más claro si revisáis las diapositivas anteriores (39 y 43).

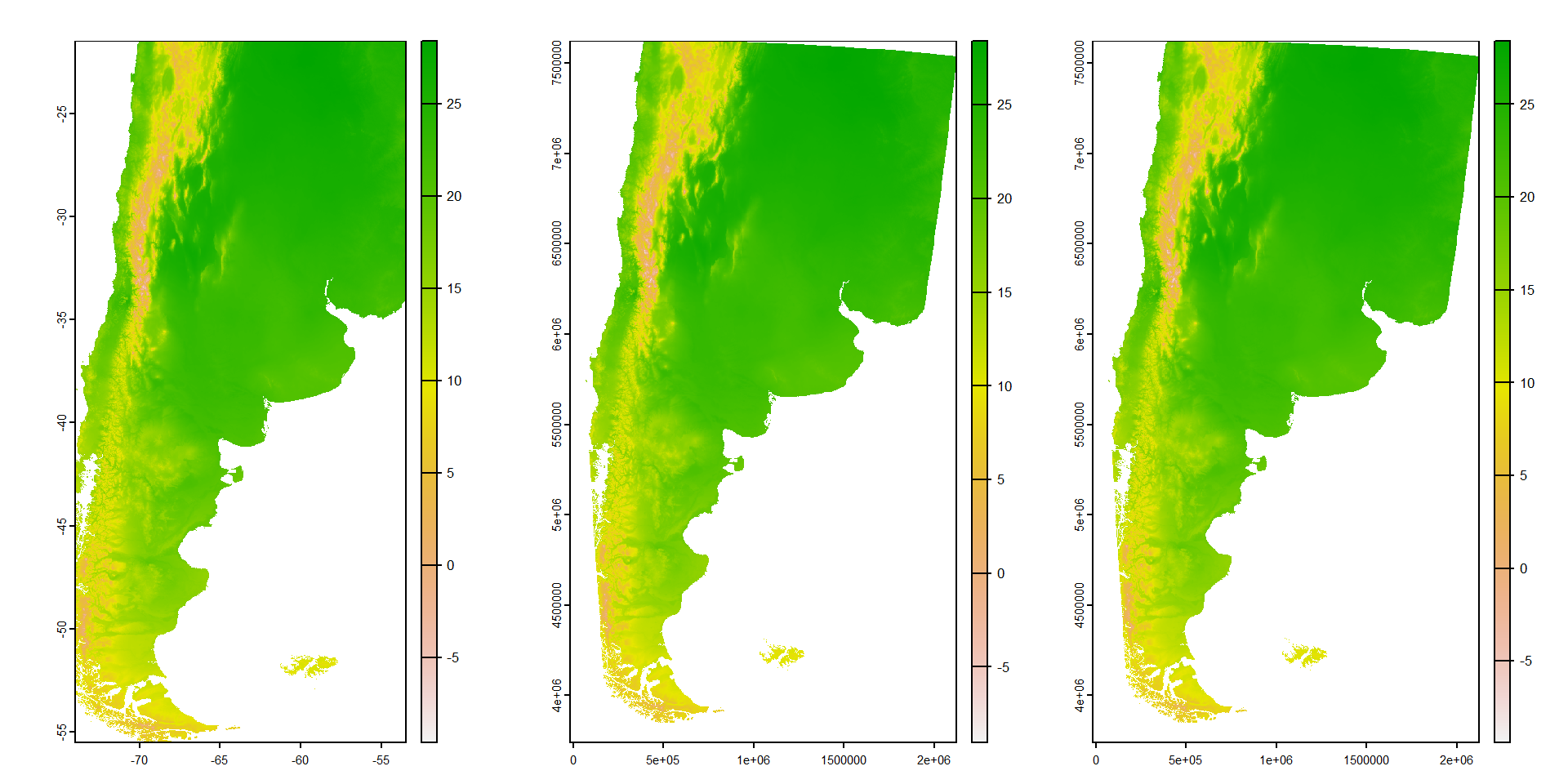
Para controlar el número de pixeles y su resolución podemos crear una “plantilla”

plantilla <- rast(tavg_utm19s)
res(plantilla) <- 800
plantilla

class       : SpatRaster 
dimensions  : 4853, 2673, 12  (nrow, ncol, nlyr)
resolution  : 800, 800  (x, y)
extent      : -18378.29, 2120022, 3739870, 7622270  (xmin, xmax, ymin, ymax)
coord. ref. : WGS 84 / UTM zone 19S (EPSG:32719) 

tavg_utm19s_plantilla <- project(tavg, plantilla)

|---------|---------|---------|---------|
=========================================
                                          

tavg_utm19s_plantilla

class       : SpatRaster 
dimensions  : 4853, 2673, 12  (nrow, ncol, nlyr)
resolution  : 800, 800  (x, y)
extent      : -18378.29, 2120022, 3739870, 7622270  (xmin, xmax, ymin, ymax)
coord. ref. : WGS 84 / UTM zone 19S (EPSG:32719) 
source      : spat_6a7843063ab8_27256.tif 
names       : ARG_w~avg_1, ARG_w~avg_2, ARG_w~avg_3, ARG_w~avg_4, ARG_w~avg_5, ARG_w~avg_6, ... 
min values  :   -10.77633,   -11.47463,   -12.17463,   -14.20292,   -16.40292,   -19.51049, ... 
max values  :    29.20000,    28.40000,    27.30000,    25.00000,    22.20000,    20.94564, ... 

Veamos el resultado

par(mfrow = c(1, 3))
plot(tavg[[2]])
plot(tavg_utm19s[[2]])
plot(tavg_utm19s_plantilla[[2]])

Momento de practicar por vuestra cuenta

Ejercicios de clase

Parte 2. Manejo de datos ráster

Manipular datos espaciales

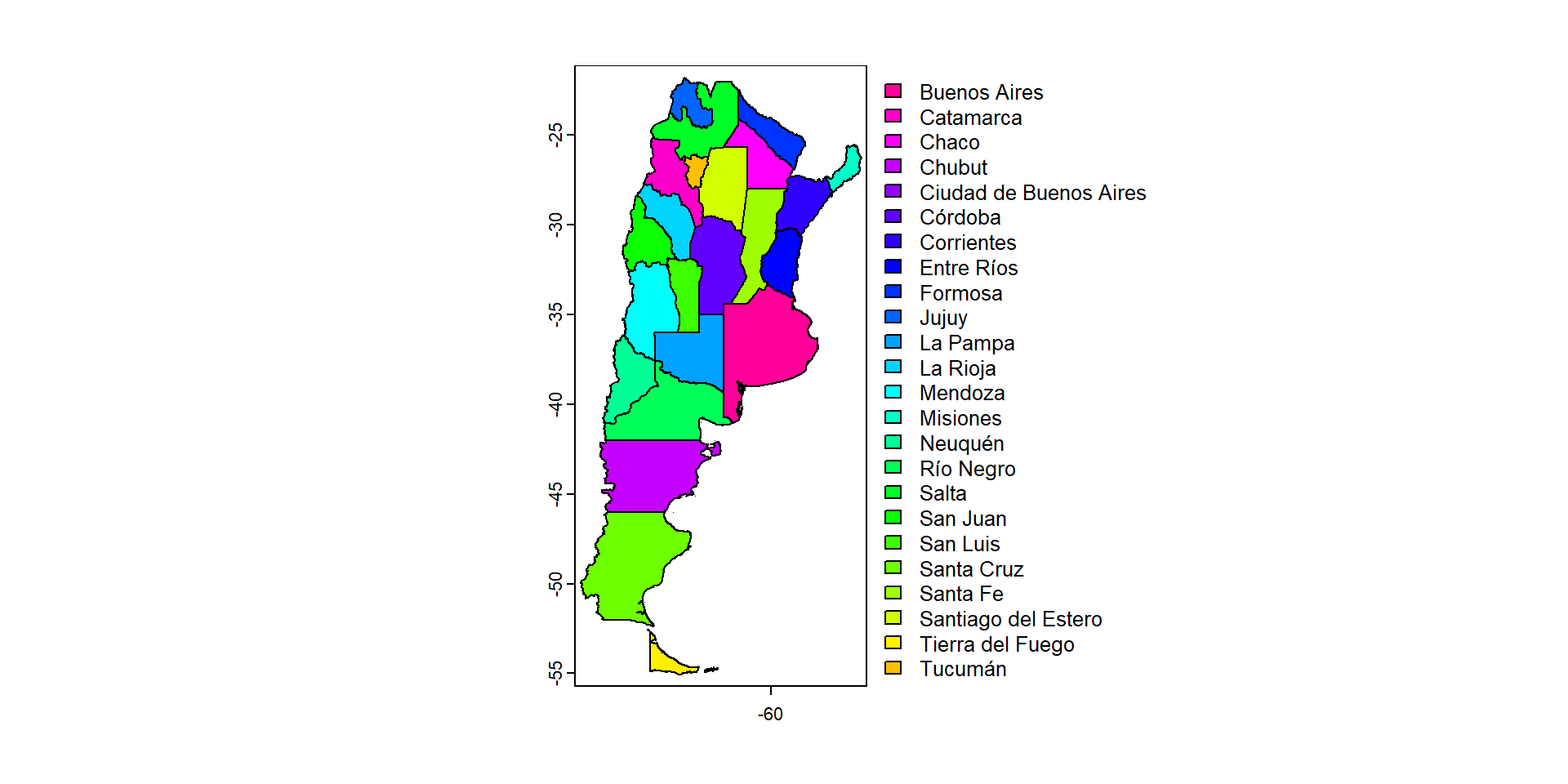
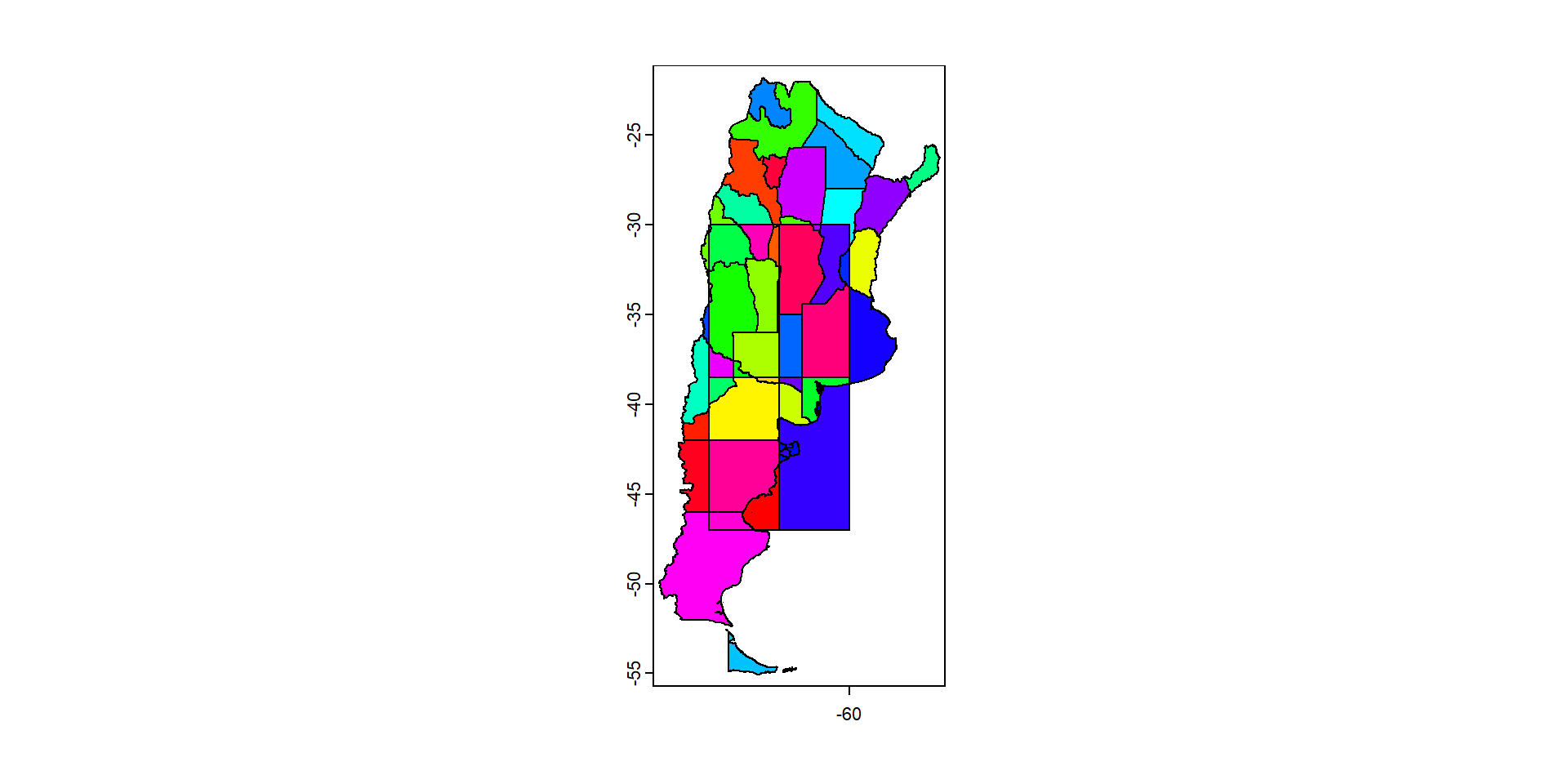
Podemos dibujar los mapas en base a información de los atributos

plot(arg, "NAME_1")

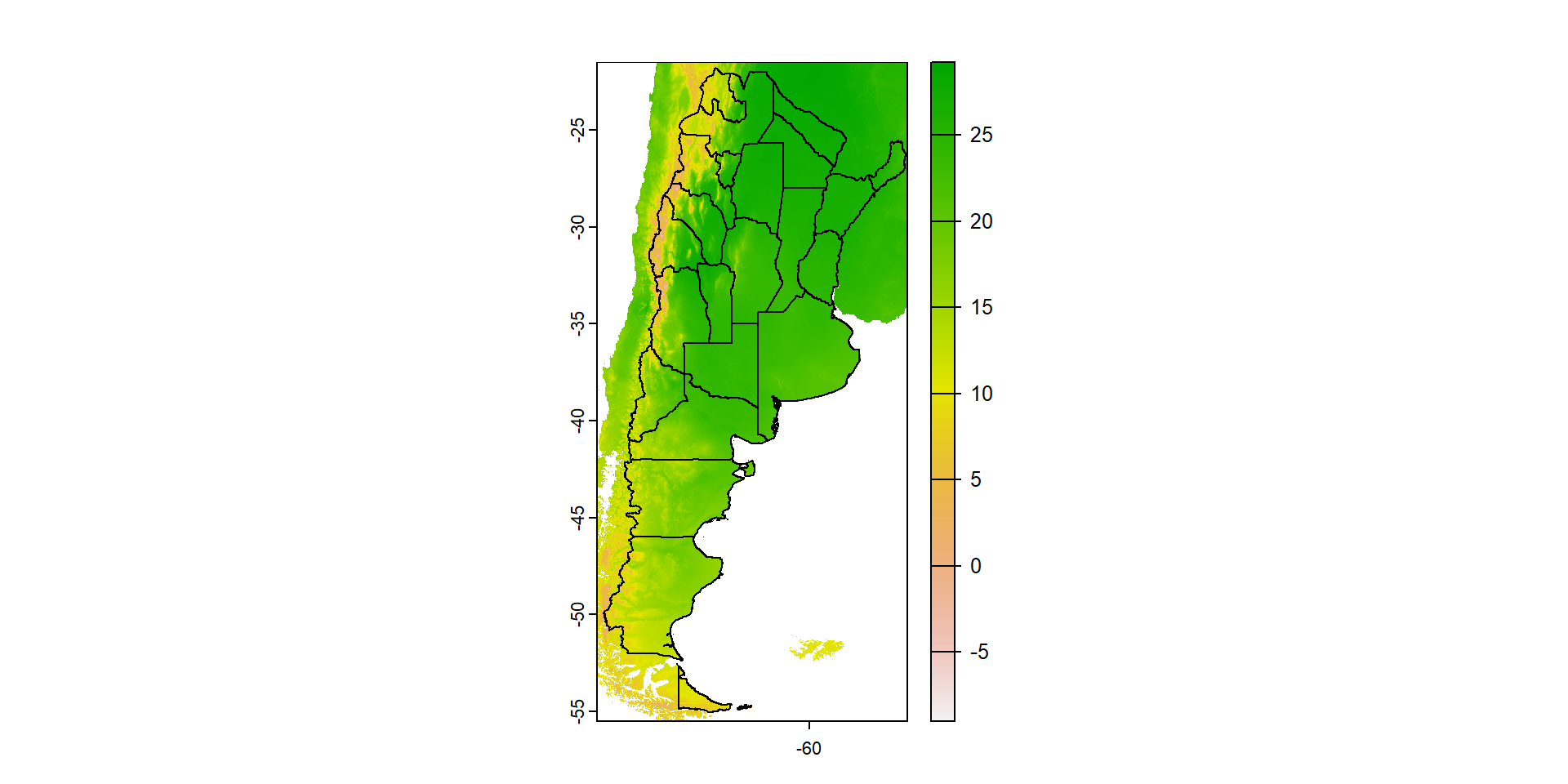
Podemos combinar información ráster y vectorial en el mismo gráfico

plot(tavg[[1]])
plot(arg, add = TRUE)

También se puede extraer información de atributos para trabajar con ella

d <- as.data.frame(arg)
head(d)

    GID_1 GID_0   COUNTRY                 NAME_1
1 ARG.1_1   ARG Argentina           Buenos Aires
2 ARG.2_1   ARG Argentina              Catamarca
3 ARG.3_1   ARG Argentina                  Chaco
4 ARG.4_1   ARG Argentina                 Chubut
5 ARG.5_1   ARG Argentina Ciudad de Buenos Aires
6 ARG.6_1   ARG Argentina                Córdoba
                         VARNAME_1 NL_NAME_1           TYPE_1        ENGTYPE_1
1              Baires|Buenos Ayres      <NA>        Provincia         Province
2                             <NA>      <NA>        Provincia         Province
3   El Chaco|Presidente Juan Peron      <NA>        Provincia         Province
4                             <NA>      <NA>        Provincia         Province
5 BUENOS AIRES D.F.|Capital Federa      <NA> Distrito Federal Federal District
6                          Cordova      <NA>        Provincia         Province
  CC_1 HASC_1 ISO_1
1 <NA>  AR.BA  AR-B
2 <NA>  AR.CT  AR-K
3 <NA>  AR.CC  AR-H
4 <NA>  AR.CH  AR-U
5 <NA>  AR.DF  <NA>
6 <NA>  AR.CB  <NA>

O puedo extraer la información de uno sólo de los atributos

arg$NAME_1

 [1] "Buenos Aires"           "Catamarca"              "Chaco"                 
 [4] "Chubut"                 "Ciudad de Buenos Aires" "Córdoba"               
 [7] "Corrientes"             "Entre Ríos"             "Formosa"               
[10] "Jujuy"                  "La Pampa"               "La Rioja"              
[13] "Mendoza"                "Misiones"               "Neuquén"               
[16] "Río Negro"              "Salta"                  "San Juan"              
[19] "San Luis"               "Santa Cruz"             "Santa Fe"              
[22] "Santiago del Estero"    "Tierra del Fuego"       "Tucumán"               

arg[, "NAME_1"]

 class       : SpatVector 
 geometry    : polygons 
 dimensions  : 24, 1  (geometries, attributes)
 extent      : -73.56056, -53.59184, -55.06153, -21.78137  (xmin, xmax, ymin, ymax)
 coord. ref. : lon/lat WGS 84 (EPSG:4326) 
 names       :       NAME_1
 type        :        <chr>
 values      : Buenos Aires
                  Catamarca
                      Chaco

Warning

Notad que en este caso, las dos formas de extraer información no se comportan exactamente igual

También podemos extraer las características geográficas (espaciales)

g <- geom(arg_utm19s) 
head(g)

     geom part       x       y hole
[1,]    1    1 1084262 5487852    0
[2,]    1    1 1084239 5487854    0
[3,]    1    1 1084236 5487823    0
[4,]    1    1 1084213 5487825    0
[5,]    1    1 1084206 5487732    0
[6,]    1    1 1084159 5487735    0

Es posible incorporar información a nuestros datos vectoriales

perim(arg)

 [1] 6542992.70 2141772.81 1833193.58 4072812.99   75022.34 1898965.96
 [7] 1546899.19 1391962.59 1887284.93 1410538.99 1816741.56 1613964.82
[13] 2160729.22 1272355.56 2006884.02 2829645.14 3018996.89 1897253.64
[19] 1379291.29 3552443.52 2159600.76 1709915.38 2035550.57  814874.32

arg$perimetro <- perim(arg)

expanse(arg)

 [1] 307005689751 101325015569  99764195922 224358261357    211011750
 [6] 164663835095  88958640476  78008027779  75592720001  53125295415
[11] 142947760813  91104159966 148772281932  29980009644  94504843837
[16] 202539975187 155196050532  88821613819  75844534099 242892543838
[21] 133097028860 136911867268  20884464648  22539627987

arg$area <- expanse(arg)

¿Qué pasa si quiero borrar una columna?

arg$area <- NULL

A veces tenemos los datos en una tabla aparte

Note

Me descargué datos del censo poblacional del país

d <- read.csv("data/c2022_tp_c_resumen.csv", 
              header = TRUE, 
              encoding = "latin1")
d

                provincia poblacion
1  Ciudad de Buenos Aires   3121707
2            Buenos Aires  17523996
3               Catamarca    429562
4                   Chaco   1129606
5                  Chubut    592621
6                 Córdoba   3840905
7              Corrientes   1212696
8              Entre Ríos   1425578
9                 Formosa    607419
10                  Jujuy    811611
11               La Pampa    361859
12               La Rioja    383865
13                Mendoza   2043540
14               Misiones   1278873
15                Neuquén    710814
16              Río Negro    750768
17                  Salta   1441351
18               San Juan    822853
19               San Luis    542069
20             Santa Cruz    337226
21               Santa Fe   3544908
22    Santiago del Estero   1060906
23       Tierra del Fuego    185732
24                Tucumán   1731820

Podemos vincularla con los datos espaciales

Para vincularla necesitamos un campo en común

arg <- merge(arg, d, 
             by.x = "NAME_1", 
             by.y = "provincia")
arg

 class       : SpatVector 
 geometry    : polygons 
 dimensions  : 24, 13  (geometries, attributes)
 extent      : -73.56056, -53.59184, -55.06153, -21.78137  (xmin, xmax, ymin, ymax)
 coord. ref. : lon/lat WGS 84 (EPSG:4326) 
 names       :       NAME_1   GID_1 GID_0   COUNTRY       VARNAME_1 NL_NAME_1
 type        :        <chr>   <chr> <chr>     <chr>           <chr>     <chr>
 values      : Buenos Aires ARG.1_1   ARG Argentina Baires|Buenos ~        NA
                  Catamarca ARG.2_1   ARG Argentina              NA        NA
                      Chaco ARG.3_1   ARG Argentina El Chaco|Presi~        NA
    TYPE_1 ENGTYPE_1  CC_1 HASC_1 (and 3 more)
     <chr>     <chr> <chr>  <chr>             
 Provincia  Province    NA  AR.BA             
 Provincia  Province    NA  AR.CT             
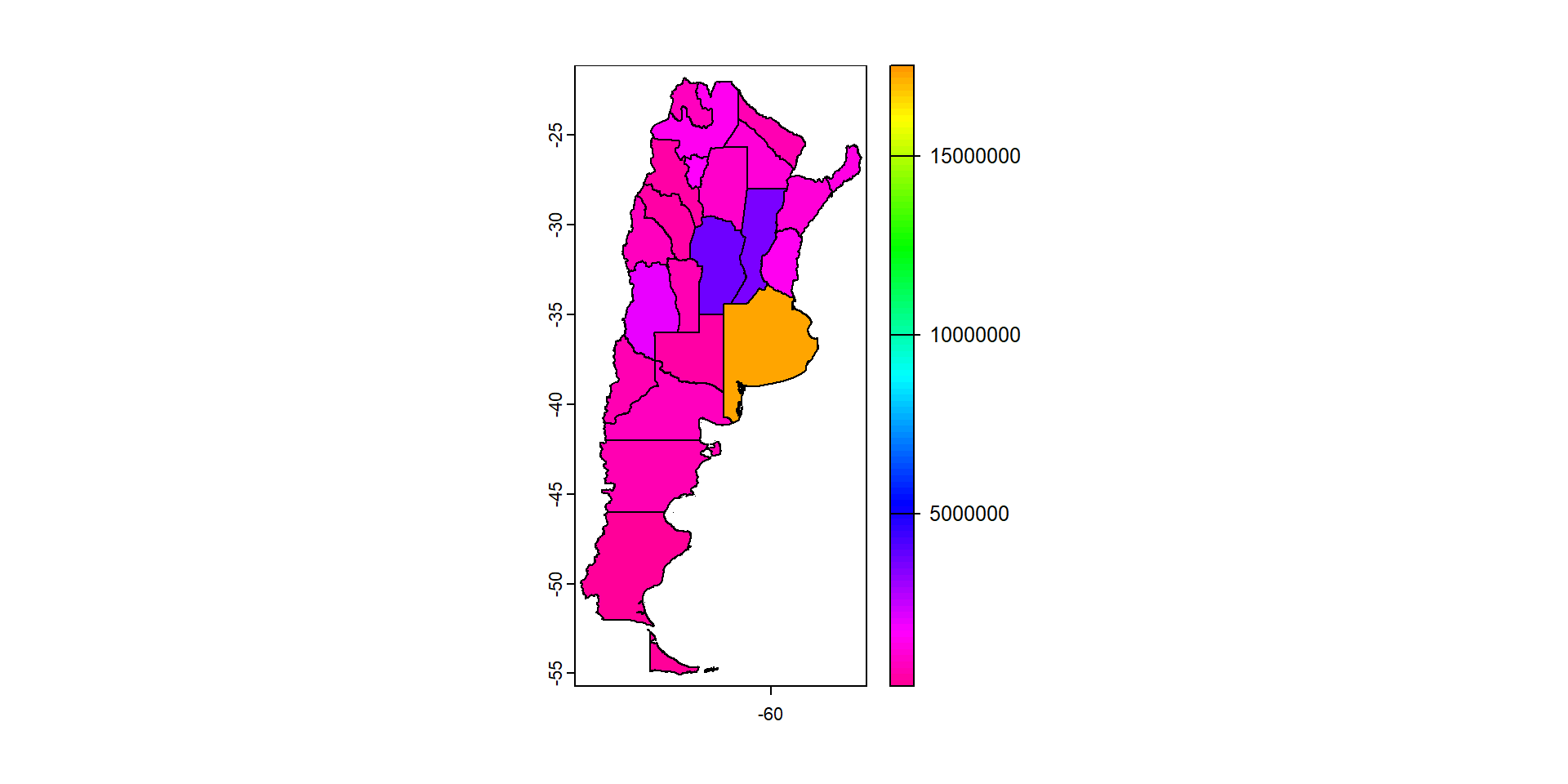
 Provincia  Province    NA  AR.CC             

Veamos la población argentina por provincias

plot(arg, "poblacion", type = "continuous")

A veces necesitamos fusionar las formas de varios polígonos (o líneas) en uno de mayor tamaño

arg_0 <- aggregate(arg, by = "COUNTRY") 
plot(arg_0, col = "white", lwd = 2, border = "cyan")

Los objetos ráster también se pueden agregar

Note

La agregación aquí trabaja a nivel de píxel, por lo que se usan para cambiar la resolución de los datos.

tavg_10 <- aggregate(tavg, fact = 100, fun = "mean", na.rm = TRUE)
par(mfrow = c(1, 2))
plot(tavg[[1]])
plot(tavg_10[[1]])

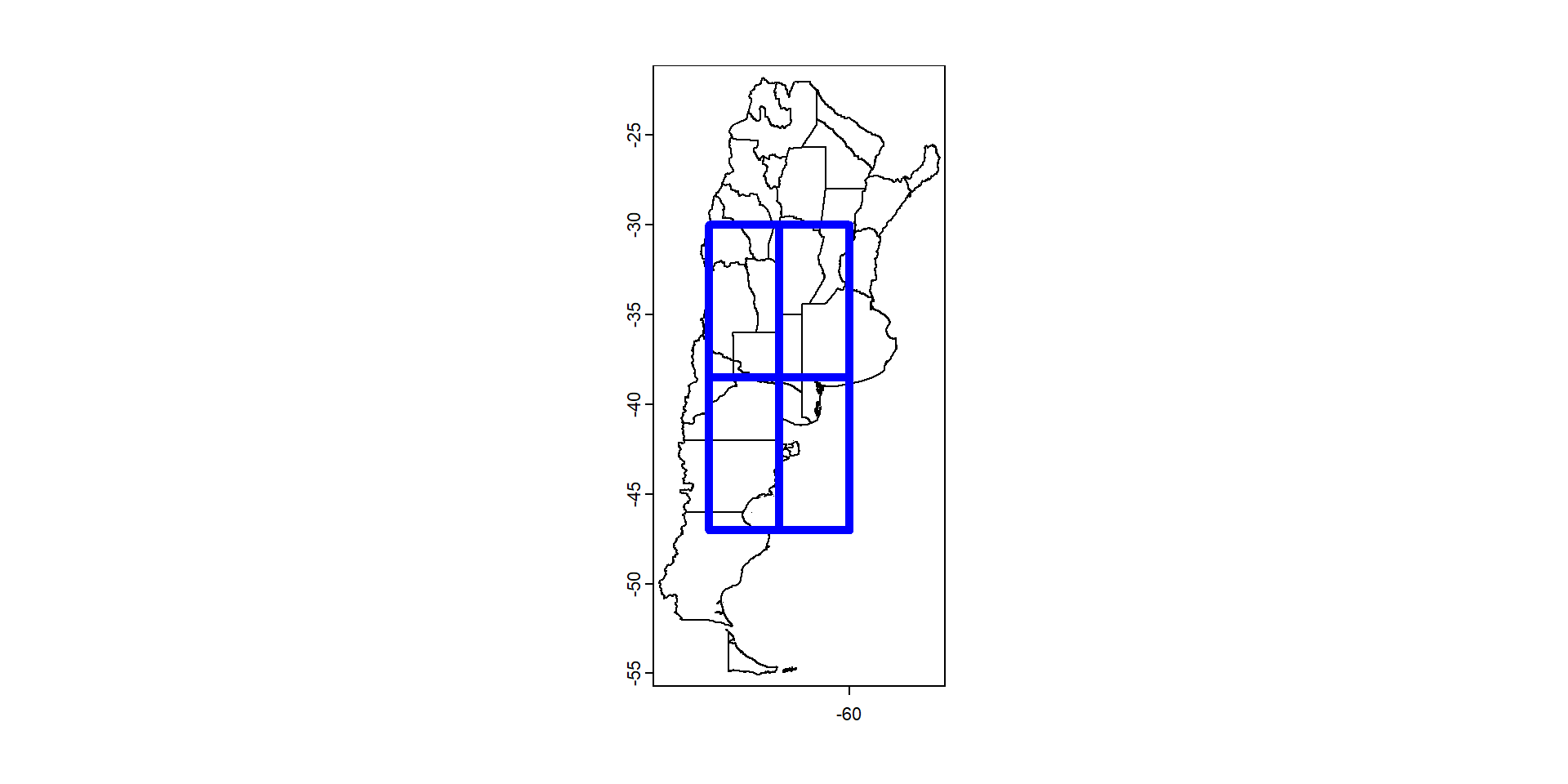
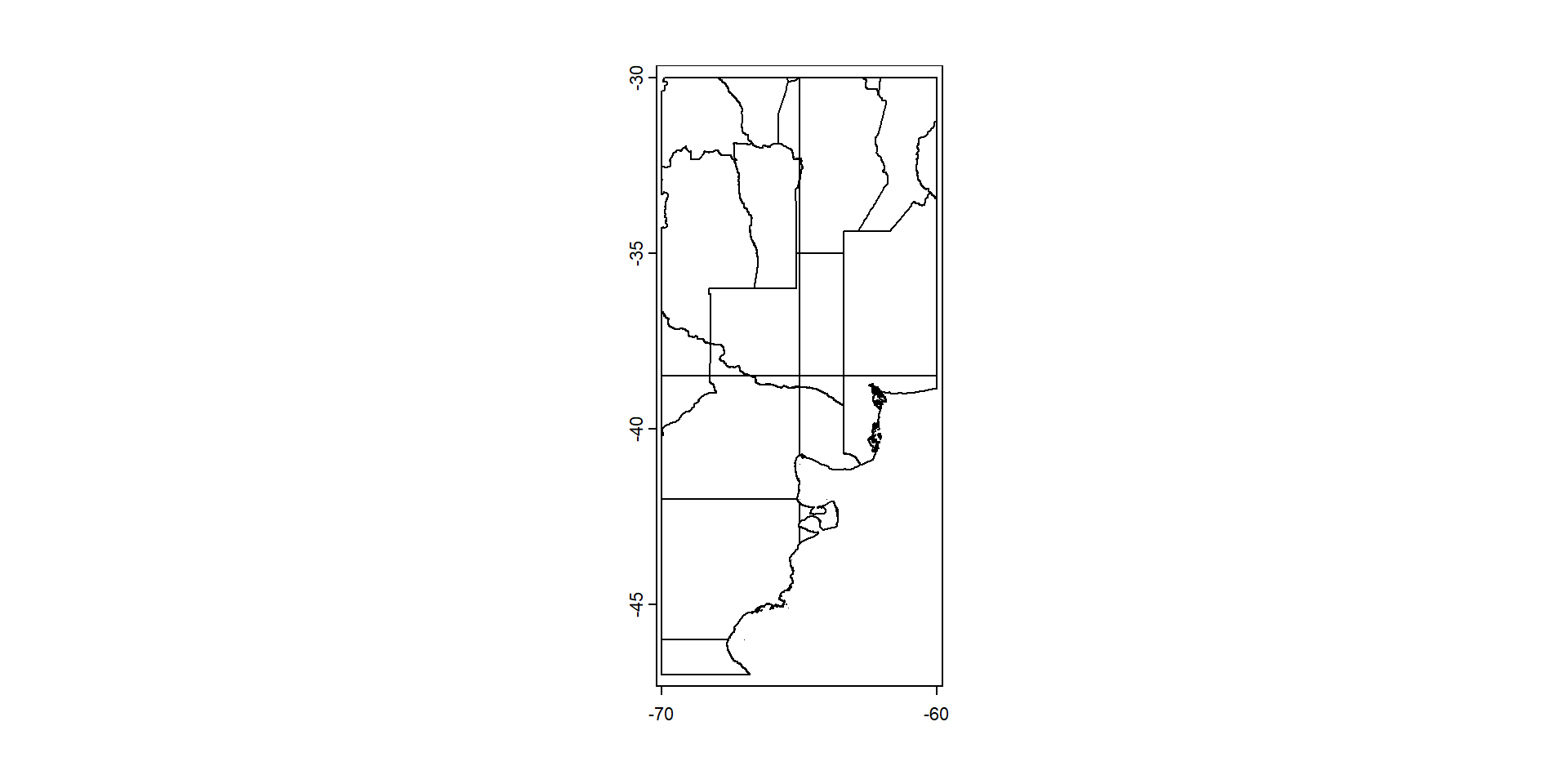
Podemos usar una capa vectorial como máscara para seleccionar objetos dentro de otra capa vectorial

clip <- rast(ext = c(-70, -60, -47, -30), nrow = 2, ncol = 2)
values(clip) <- 1:4
names(clip) <- "Zona"
clip <- as.polygons(clip)
clip 

 class       : SpatVector 
 geometry    : polygons 
 dimensions  : 4, 1  (geometries, attributes)
 extent      : -70, -60, -47, -30  (xmin, xmax, ymin, ymax)
 coord. ref. : lon/lat WGS 84 (CRS84) (OGC:CRS84) 
 names       :  Zona
 type        : <int>
 values      :     1
                   2
                   3

Veamos que aspecto presentan las dos capas

plot(arg) 
plot(clip, add = TRUE, border = "blue", lwd = 5) 

Hagamos la intersección y veamos el resultado

arg_clip <- intersect(arg, clip) 
plot(arg_clip)

Los objetos ráster también se pueden cortar con un vectorial

tavg_arg <- mask(tavg, arg)

|---------|---------|---------|---------|
=========================================
                                          

par(mfrow = c(1, 2))
plot(tavg[[1]])
plot(tavg_arg[[1]])

Otras veces necesitamos combinar las formas de dos objetos vectoriales diferentes

u <- union(arg, clip)
plot(u, col = sample(rainbow(length(u))))

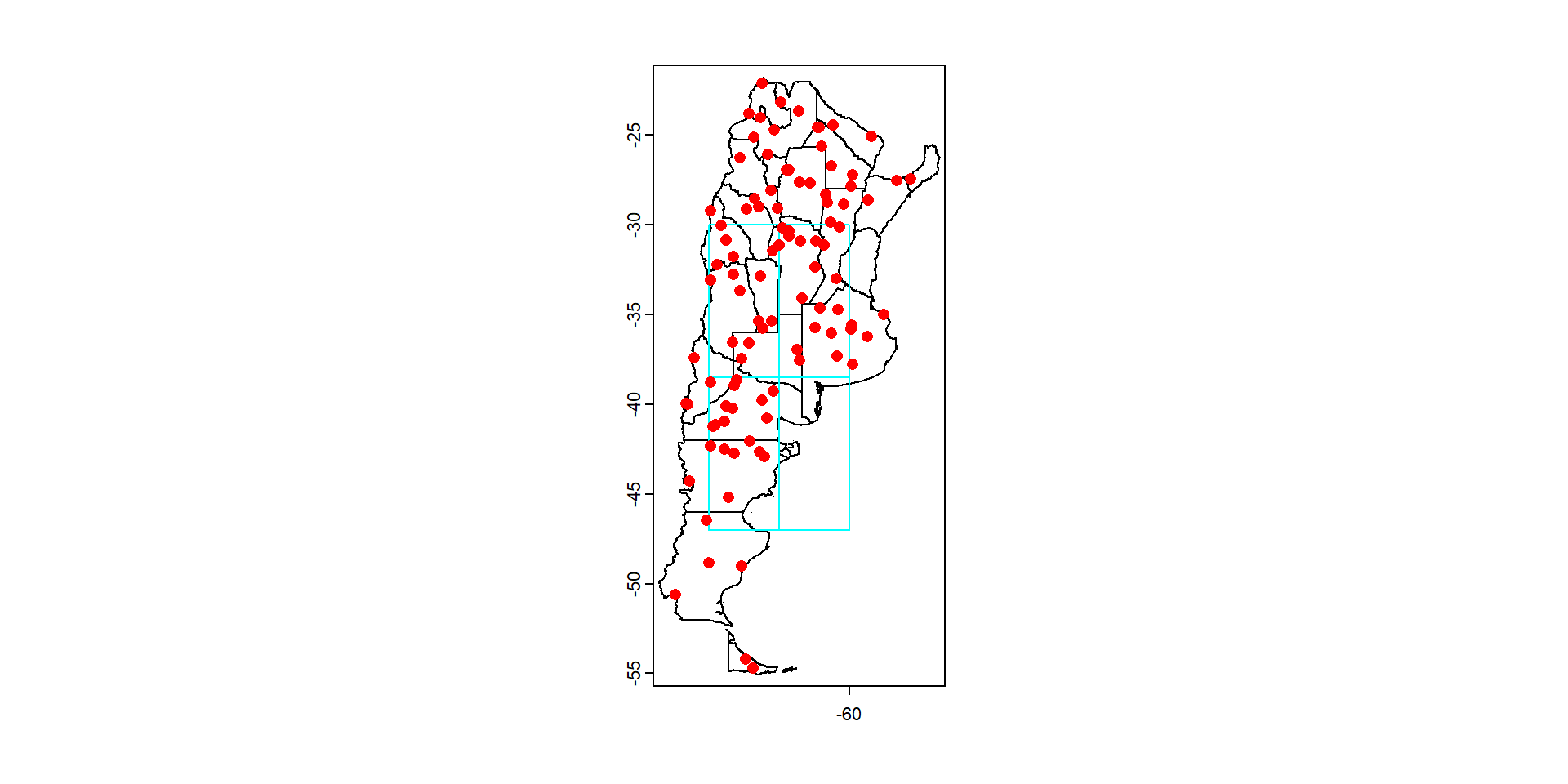
Es muy útil extraer información de una capa vectorial en los puntos, líneas o polígonos de otra capa vectorial

Para ello creamos una capa de puntos cualquiera

pnts <- spatSample(arg, 100)

plot(arg)
plot(clip, add = TRUE, border = "cyan")
plot(pnts, add = TRUE, col = "red")

Veamos los valores de las capas en los puntos

pnts_arg <- extract(arg, pnts)
head(pnts_arg)

  id.y       NAME_1    GID_1 GID_0   COUNTRY           VARNAME_1 NL_NAME_1
1    1    Catamarca  ARG.2_1   ARG Argentina                <NA>      <NA>
2    2      Neuquén ARG.15_1   ARG Argentina             Neuquén      <NA>
3    3 Buenos Aires  ARG.1_1   ARG Argentina Baires|Buenos Ayres      <NA>
4    4       Chubut  ARG.4_1   ARG Argentina                <NA>      <NA>
5    5        Salta ARG.17_1   ARG Argentina                <NA>      <NA>
6    6      Córdoba  ARG.6_1   ARG Argentina             Cordova      <NA>
     TYPE_1 ENGTYPE_1 CC_1 HASC_1 ISO_1 perimetro poblacion
1 Provincia  Province <NA>  AR.CT  AR-K   2141773    429562
2 Provincia  Province <NA>  AR.NQ  <NA>   2006884    710814
3 Provincia  Province <NA>  AR.BA  AR-B   6542993  17523996
4 Provincia  Province <NA>  AR.CH  AR-U   4072813    592621
5 Provincia  Province <NA>  AR.SA  AR-A   3018997   1441351
6 Provincia  Province <NA>  AR.CB  <NA>   1898966   3840905

pnts_clip <- extract(clip, pnts)
head(pnts_clip)

  id.y Zona
1    1   NA
2    2    3
3    3   NA
4    4    3
5    5   NA
6    6    2

Igual podemos hacer con respecto a los valores de los píxeles en cada punto de un vectorial

pnts_tavg <- extract(tavg, pnts)
head(pnts_tavg)

  ID ARG_wc2.1_30s_tavg_1 ARG_wc2.1_30s_tavg_2 ARG_wc2.1_30s_tavg_3
1  1                 25.6                 24.3                 22.3
2  2                 18.9                 18.0                 15.0
3  3                 23.1                 22.1                 20.5
4  4                 18.3                 17.5                 14.5
5  5                  9.6                  9.0                  8.5
6  6                 23.9                 22.6                 20.0
  ARG_wc2.1_30s_tavg_4 ARG_wc2.1_30s_tavg_5 ARG_wc2.1_30s_tavg_6
1                 18.9                 15.4                 11.9
2                 10.7                  7.2                  4.3
3                 16.8                 13.3                 10.3
4                 10.1                  6.3                  3.2
5                  6.3                  3.7                  0.8
6                 16.4                 12.9                  9.3
  ARG_wc2.1_30s_tavg_7 ARG_wc2.1_30s_tavg_8 ARG_wc2.1_30s_tavg_9
1                 11.6                 14.3                 17.6
2                  4.0                  5.3                  7.5
3                  9.5                 11.1                 13.0
4                  3.1                  4.9                  7.4
5                  0.9                  2.3                  4.7
6                  8.7                 10.6                 13.3
  ARG_wc2.1_30s_tavg_10 ARG_wc2.1_30s_tavg_11 ARG_wc2.1_30s_tavg_12
1                  20.9                  23.3                  25.5
2                  11.3                  15.0                  17.7
3                  15.8                  18.4                  21.6
4                  10.9                  14.4                  16.9
5                   6.6                   8.2                   9.5
6                  16.8                  19.9                  23.0

Warning

Fijaros que extrae un valor de cada capa del ráster stack

También funciona con polígonos

prov_tavg <- extract(tavg, arg, fun = "mean", bind = TRUE, na.rm = TRUE)
plot(prov_tavg, "ARG_wc2.1_30s_tavg_1")

Los objetos ráster se puede operar matemáticamente con ellos para generar estadísticos

min, max, mean, prod, sum, median, cv, range, any y all

min_tavg <- min(tavg)

|---------|---------|---------|---------|
=========================================
                                          

plot(min_tavg)

También hay multitud de funciones avanzadas propias de un SIG, tanto para vectoriales como ráster

crop, trim, merge, disagg, resample, classify o cover

El paquete gdistance ofrece análisis de distancias complejos (least cost path, etcétera)

Last but not least! Se pueden transformar datos vectoriales en ráster…

arg_raster <- rasterize(arg, tavg, field = "NAME_1")
class(arg_raster)

[1] "SpatRaster"
attr(,"package")
[1] "terra"

plot(arg_raster)

… y viceversa

as.polygons(tavg[[1]])

 class       : SpatVector 
 geometry    : polygons 
 dimensions  : 41, 1  (geometries, attributes)
 extent      : -74, -53.5, -55.5, -21.5  (xmin, xmax, ymin, ymax)
 coord. ref. : lon/lat WGS 84 (EPSG:4326) 
 names       : ARG_wc2.1_30s_tavg_1
 type        :                <int>
 values      :                  -11
                                -10
                                 -9

Hora de trabajar por vuestra cuenta…

Ejercicios de clase

Parte 3. Manipulación de datos ráster y vectoriales