Análisis multivariante en R

Diego Nieto Lugilde

Universidad de Córdoba (España)

2024-10-16

Preparación de datos

Análisis multivariante usa datos tabulados

Matriz de comunidades (sitios x especies)
	sp_1	sp_2	…	sp_n
site_1	1	0	…	1
site_2	0	0	…	1
…	…	…	…	…
site_n	0	1	…	1

También los datos de las variables ambientales

Matriz de variables (sitios x variables)
	v_1	v_2	…	v_n
site_1	1	0	…	1
site_2	0	0	…	1
…	…	…	…	…
site_n	0	1	…	1

Cargando de datos en R

library(xlsx)
com <- read.xlsx("data/Inventarios.xlsx", sheetIndex = 1, row.names = 1)
head(com)

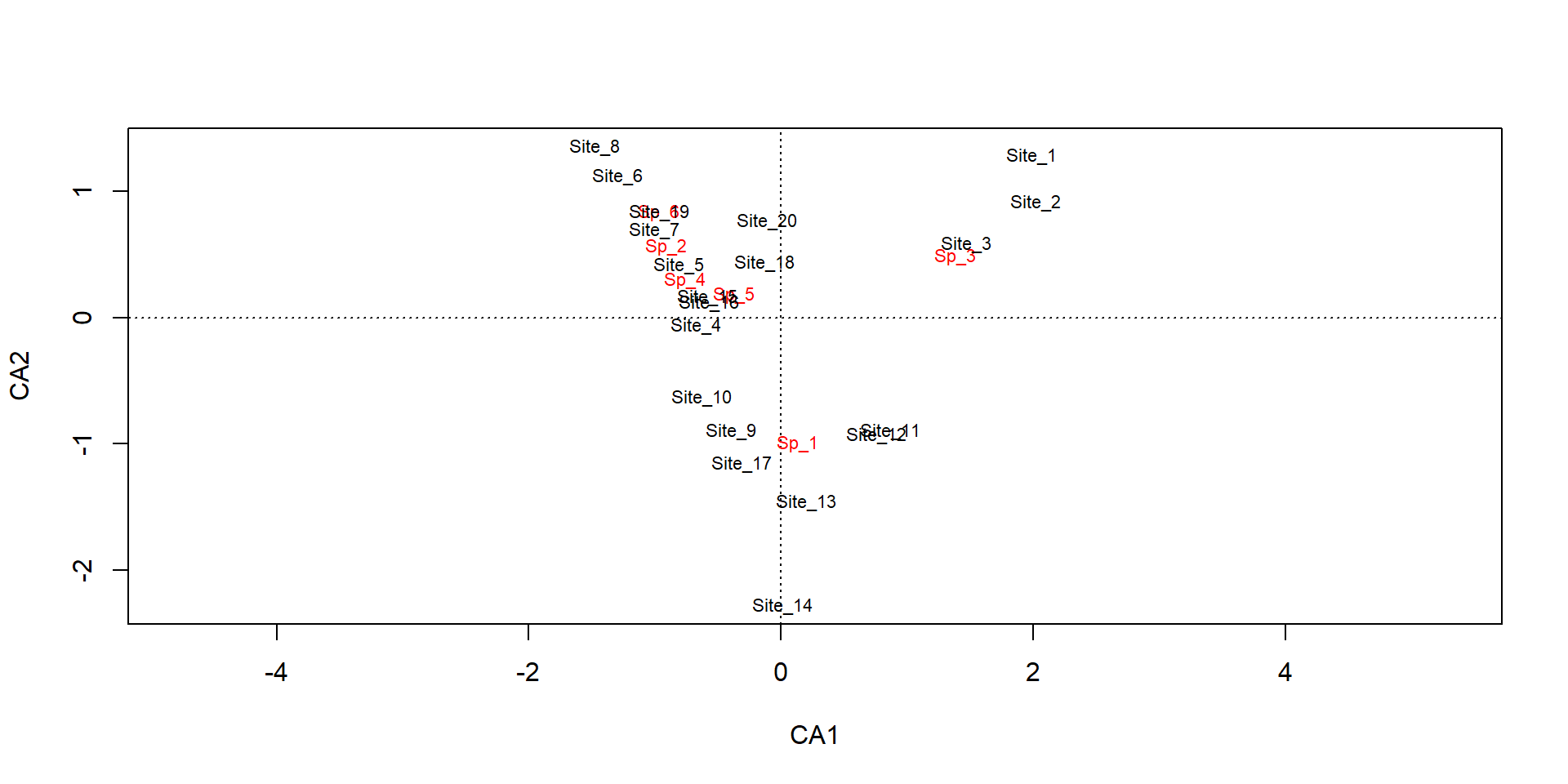
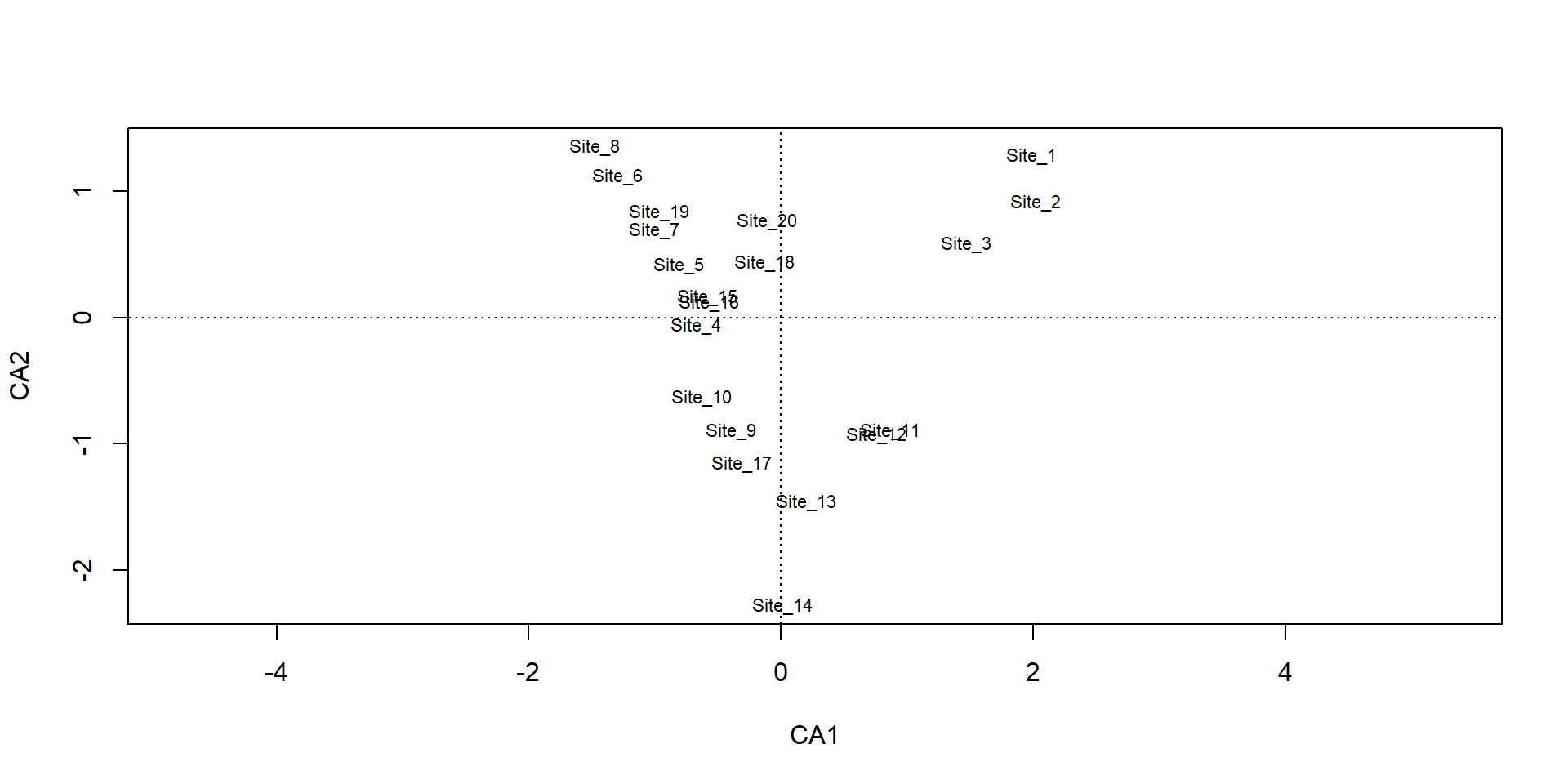
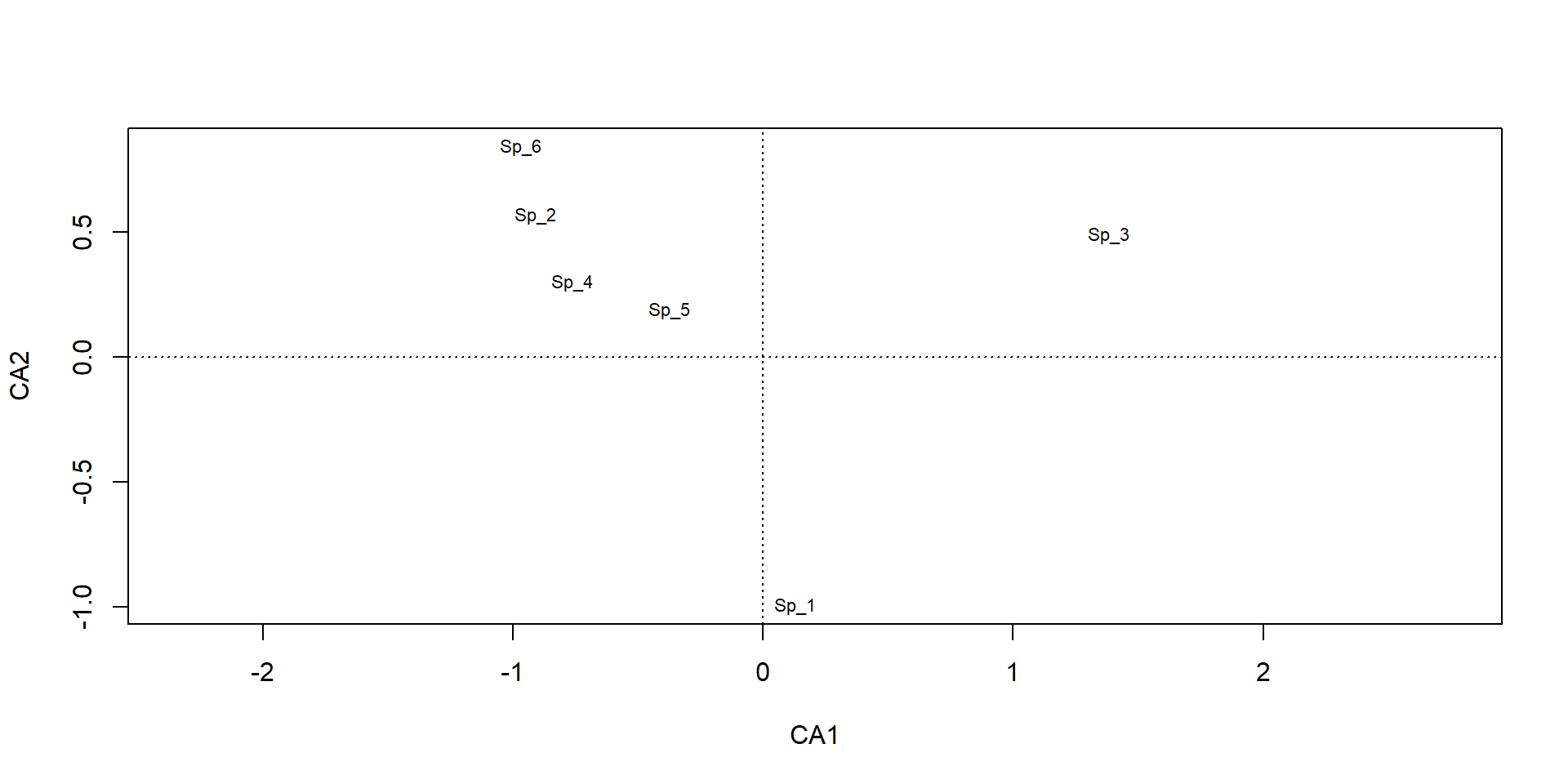
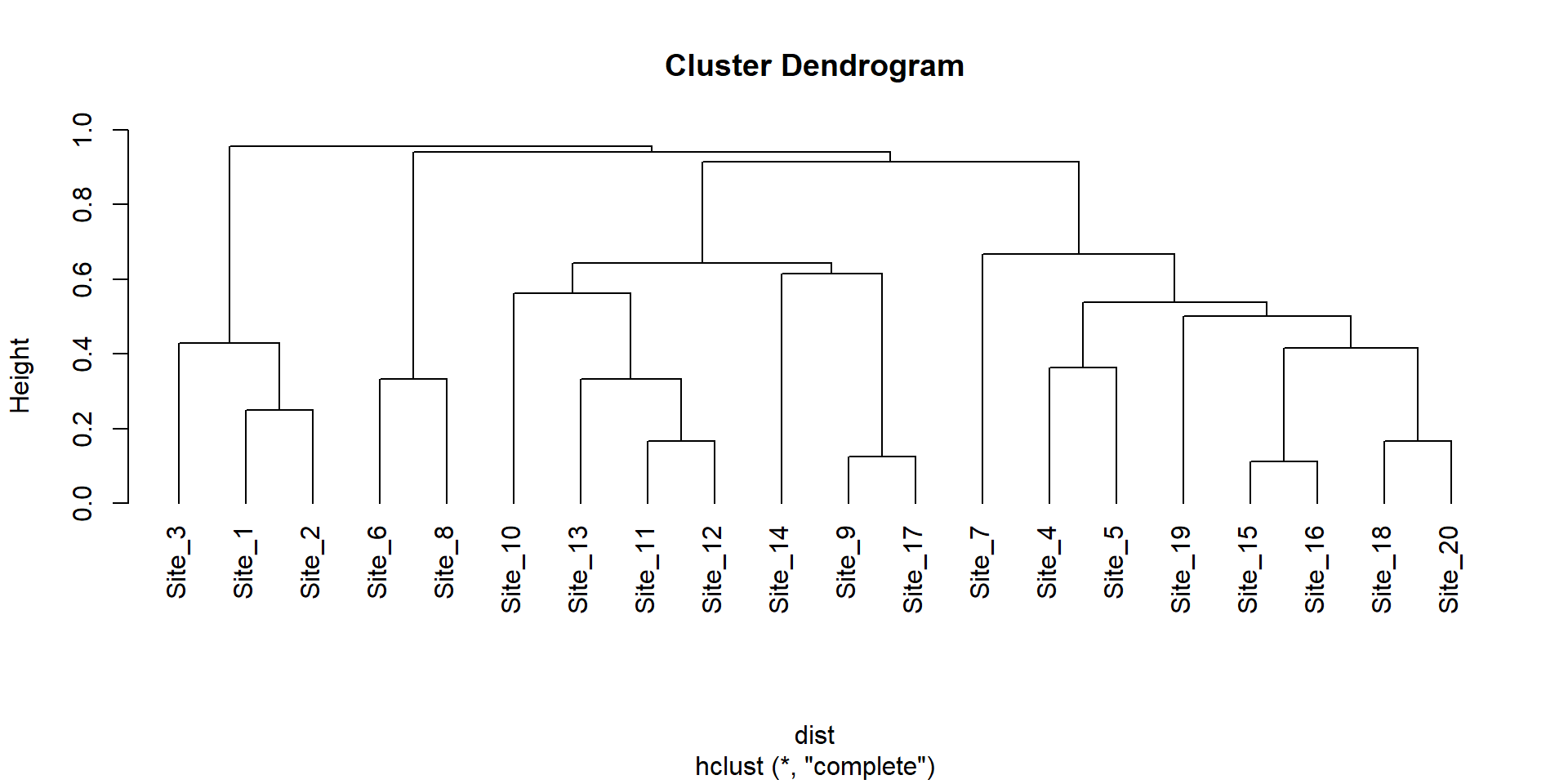
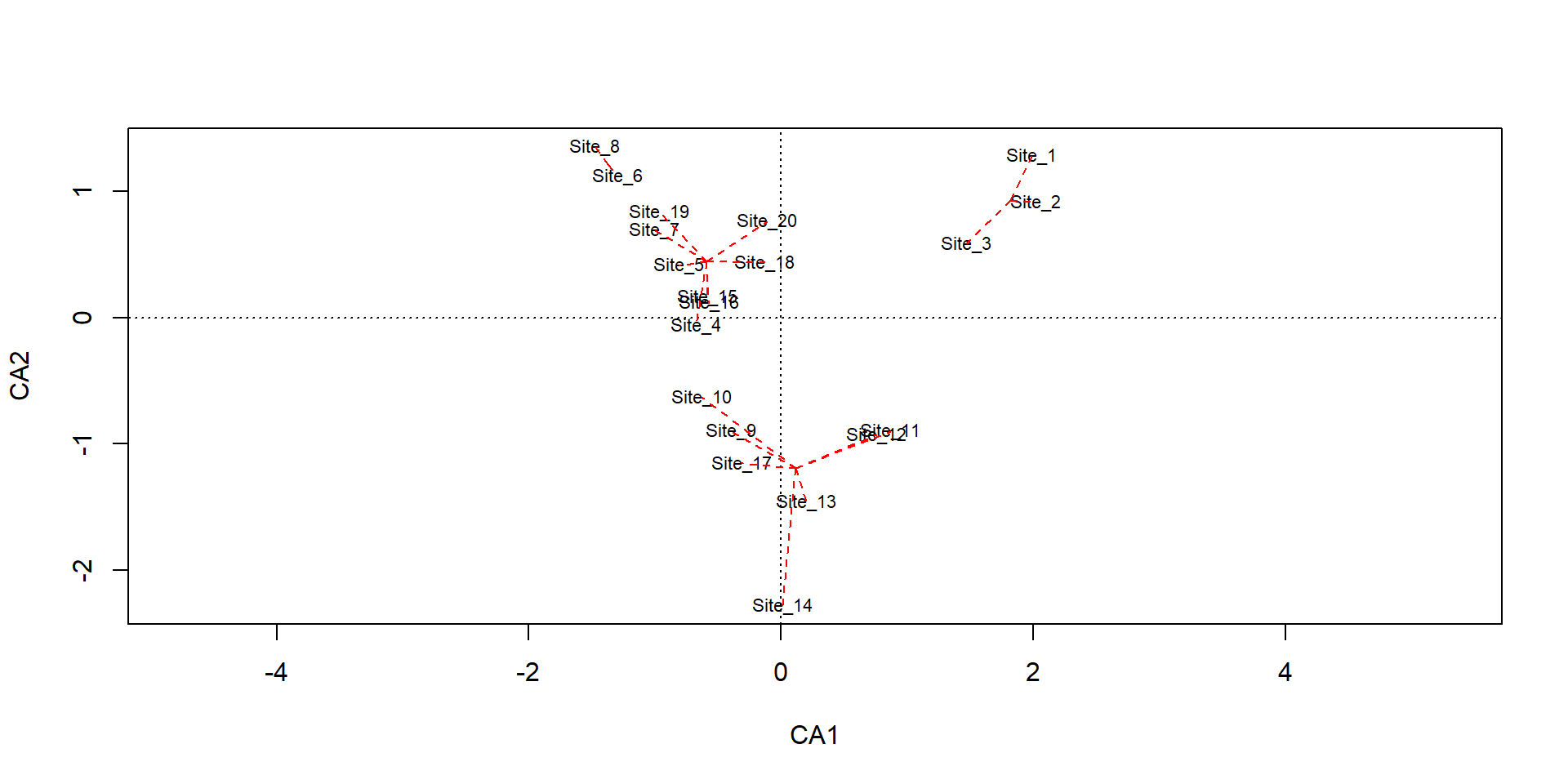
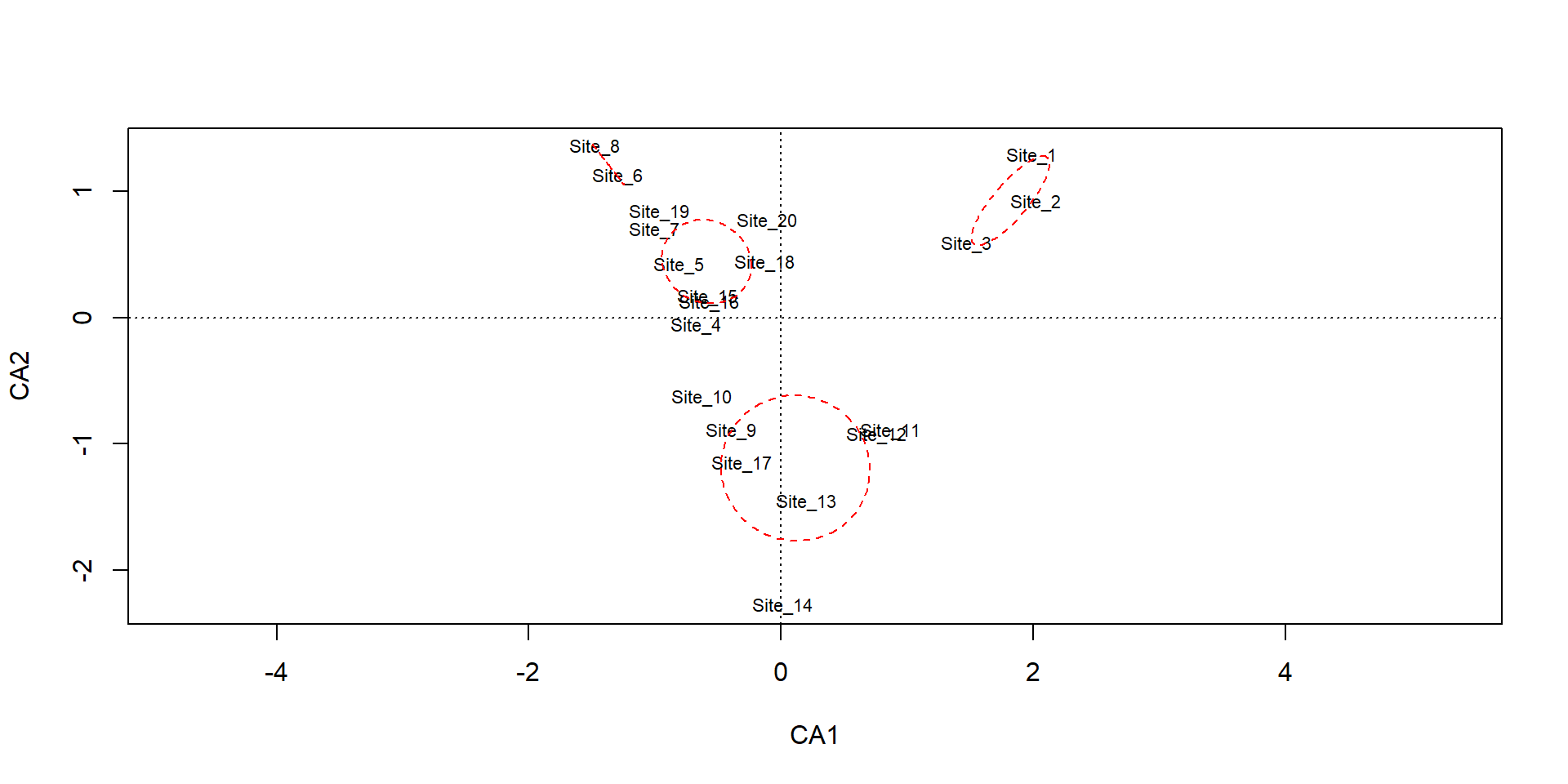
       Sp_1 Sp_2 Sp_3 Sp_4 Sp_5 Sp_6
Site_1    0    0    9    0    2    0
Site_2    1    0    8    0    1    0
Site_3    2    1    7    0    1    0
Site_4    2    1    0    1    5    0
Site_5    1    2    0    0    6    0
Site_6    0    4    0    2    3    0

env <- read.xlsx("data/Variables.xlsx", sheetIndex = 1, row.names = 1)
head(env)

              v1         v2         v3
Site_1 5.1789918 -0.4380167  2.8471131
Site_2 4.4714402  1.8806640 -0.3560559
Site_3 2.9379526 -0.3054643  3.2177157
Site_4 0.7354044 -1.9925002  1.2593483
Site_5 2.6035489 -2.5324108  1.9391404
Site_6 0.6951173  2.8438965 -1.2821121

Los nombres de especies largos pueden saturar los gráficos

Si la identidad es irrelevante: usar nombres genéricos
- Quercus ilex: SP_1
Si la identidad de la especie es relevante: acortar
- Quercus ilex: Q_ILEX
Cornell Ecology Program (CEP) proporciona una abreviatura estandarizada:
- 8 caracteres: 4 primeros del género y 4 de la especie:
- Quercus ilex: QUERILEX

Transformación de valores de dominancia-abundancia

Índice Braun-Blanquet	Valor de Van deer Maarel
ausencia	0
r	1
+	2
1	3
2m	4
2a	5
2b	6
3	7
4	8
5	9

Datos de presencia-ausencia

Los análisis con datos de presencia-ausencia suelen ser más robustos que los de abundancia o cobertura

pres <- ifelse(com > 0, 1, 0)
head(pres)

       Sp_1 Sp_2 Sp_3 Sp_4 Sp_5 Sp_6
Site_1    0    0    1    0    1    0
Site_2    1    0    1    0    1    0
Site_3    1    1    1    0    1    0
Site_4    1    1    0    1    1    0
Site_5    1    1    0    0    1    0
Site_6    0    1    0    1    1    0

Análisis de ordenación en R

Para el análisis de vegetación en R hay un paquete muy útil: vegan

#install.packages("vegan")
library(vegan)

Análisis de componentes principales (PCA)

Aunque parezca confuso, se usa la función rda.

Note

Así se juntan la aproximación unconstrained y su equivalente constrained en la misma función. Si se especifican variables ambientales se ejecuta la versión constrained. Si no se especifican se ejecuta la versión unconstrained.

library(vegan)
com_pca <- rda(com)
com_pca

Call: rda(X = com)

              Inertia Rank
Total           25.54     
Unconstrained   25.54    6
Inertia is variance 

Eigenvalues for unconstrained axes:
   PC1    PC2    PC3    PC4    PC5    PC6 
11.855  8.544  3.847  0.941  0.325  0.027

Análisis de redundancia (RDA)

com_rda <- rda(com, env)
com_rda

Call: rda(X = com, Y = env)

              Inertia Proportion Rank
Total         25.5395     1.0000     
Constrained   14.2138     0.5565    3
Unconstrained 11.3256     0.4435    6
Inertia is variance 

Eigenvalues for constrained axes:
 RDA1  RDA2  RDA3 
7.435 6.190 0.589 

Eigenvalues for unconstrained axes:
  PC1   PC2   PC3   PC4   PC5   PC6 
8.109 1.250 1.054 0.694 0.200 0.018

Análisis de correspondencia (CA)

Aunque parezca confuso, para CA y CCA se usa la función cca.

Note

com_ca <- cca(com)
com_ca

Call: cca(X = com)

              Inertia Rank
Total           1.336     
Unconstrained   1.336    5
Inertia is scaled Chi-square 

Eigenvalues for unconstrained axes:
   CA1    CA2    CA3    CA4    CA5 
0.5359 0.3371 0.3013 0.1014 0.0600

Análisis de correspondencia sin tendencia (DCA)

Para DCA se usa la función decorana

com_dca <- decorana(com)
com_dca


Call:
decorana(veg = com) 

Detrended correspondence analysis with 26 segments.
Rescaling of axes with 4 iterations.
Total inertia (scaled Chi-square): 1.3356 

                       DCA1   DCA2    DCA3    DCA4
Eigenvalues          0.5017 0.3112 0.16425 0.17184
Additive Eigenvalues 0.5017 0.3102 0.14014 0.09521
Decorana values      0.5359 0.1160 0.05699 0.01393
Axis lengths         2.8105 1.6228 1.09955 1.12945

Análisis de correspondencia canónica (CCA)

com_cca <- cca(com, env)
com_cca

Call: cca(X = com, Y = env)

              Inertia Proportion Rank
Total          1.3356     1.0000     
Constrained    0.6556     0.4909    3
Unconstrained  0.6800     0.5091    5
Inertia is scaled Chi-square 

Eigenvalues for constrained axes:
  CCA1   CCA2   CCA3 
0.3345 0.2740 0.0471 

Eigenvalues for unconstrained axes:
   CA1    CA2    CA3    CA4    CA5 
0.4669 0.1206 0.0436 0.0395 0.0093

PCA basado en transformaciones

Para ello se transforman los datos con la función decostand

com_hel <- decostand(com, 'hellinger')

com_tbpca <- rda(com_hel)
com_tbpca

Call: rda(X = com_hel)

              Inertia Rank
Total          0.3778     
Unconstrained  0.3778    6
Inertia is variance 

Eigenvalues for unconstrained axes:
    PC1     PC2     PC3     PC4     PC5     PC6 
0.16155 0.10550 0.07101 0.03200 0.00440 0.00333

PCA basado en transformaciones

Para ello se transforman los datos con la función decostand

com_tbrda <- rda(com_hel, env)
com_tbrda

Call: rda(X = com_hel, Y = env)

              Inertia Proportion Rank
Total          0.3778     1.0000     
Constrained    0.1657     0.4387    3
Unconstrained  0.2120     0.5613    6
Inertia is variance 

Eigenvalues for constrained axes:
   RDA1    RDA2    RDA3 
0.09114 0.06063 0.01398 

Eigenvalues for unconstrained axes:
    PC1     PC2     PC3     PC4     PC5     PC6 
0.15218 0.03174 0.01660 0.00743 0.00243 0.00165

Visualizar ordenación

Es interesante observar como se disponen especies y sitios en el espacio bidimensional.

Para ello usamos la función plot sobre cualquiera de los objetos de ordenación.

plot(com_ca)

¿Gráficos sobrecargados?

Puedes representar solo ‘especies’ o ‘sitios’ con el argumento display

plot(com_ca, display = "sites")

plot(com_ca, display = "species")

Análisis de clasificación en R

Medida de disimilitud

Para calcular la disimilitud entre todos los ‘sitios’ usamos la función vegdist

dist <- vegdist(com)
dist

            Site_1     Site_2     Site_3     Site_4     Site_5     Site_6
Site_2  0.14285714                                                       
Site_3  0.27272727 0.14285714                                            
Site_4  0.80000000 0.78947368 0.60000000                                 
Site_5  0.80000000 0.78947368 0.70000000 0.22222222                      
Site_6  0.80000000 0.89473684 0.80000000 0.44444444 0.44444444           
Site_7  0.77777778 0.88235294 0.88888889 0.37500000 0.50000000 0.37500000
Site_8  0.88235294 0.87500000 0.76470588 0.60000000 0.60000000 0.20000000
Site_9  0.77777778 0.76470588 0.66666667 0.25000000 0.50000000 0.50000000
Site_10 0.81818182 0.80952381 0.63636364 0.50000000 0.50000000 0.40000000
Site_11 0.47826087 0.45454545 0.39130435 0.61904762 0.71428571 0.80952381
Site_12 0.52380952 0.50000000 0.42857143 0.57894737 0.68421053 0.78947368
Site_13 0.71428571 0.70000000 0.61904762 0.47368421 0.57894737 0.68421053
Site_14 0.90909091 0.80952381 0.72727273 0.60000000 0.80000000 0.80000000
Site_15 0.80000000 0.78947368 0.80000000 0.33333333 0.22222222 0.66666667
Site_16 0.78947368 0.77777778 0.78947368 0.29411765 0.17647059 0.64705882
Site_17 0.78947368 0.77777778 0.68421053 0.29411765 0.52941176 0.52941176
Site_18 0.65217391 0.63636364 0.65217391 0.33333333 0.33333333 0.61904762
Site_19 0.83333333 0.91304348 0.83333333 0.36363636 0.36363636 0.45454545
Site_20 0.61904762 0.70000000 0.71428571 0.36842105 0.36842105 0.57894737
            Site_7     Site_8     Site_9    Site_10    Site_11    Site_12
Site_2                                                                   
Site_3                                                                   
Site_4                                                                   
Site_5                                                                   
Site_6                                                                   
Site_7                                                                   
Site_8  0.69230769                                                       
Site_9  0.42857143 0.69230769                                            
Site_10 0.77777778 0.41176471 0.44444444                                 
Site_11 0.78947368 0.88888889 0.47368421 0.39130435                      
Site_12 0.76470588 0.87500000 0.41176471 0.33333333 0.09090909           
Site_13 0.64705882 0.87500000 0.29411765 0.33333333 0.18181818 0.20000000
Site_14 0.77777778 0.76470588 0.44444444 0.45454545 0.39130435 0.42857143
Site_15 0.50000000 0.86666667 0.50000000 0.70000000 0.71428571 0.68421053
Site_16 0.46666667 0.85714286 0.46666667 0.68421053 0.70000000 0.66666667
Site_17 0.46666667 0.71428571 0.06666667 0.36842105 0.40000000 0.33333333
Site_18 0.47368421 0.77777778 0.47368421 0.73913043 0.58333333 0.54545455
Site_19 0.40000000 0.68421053 0.60000000 0.75000000 0.84000000 0.82608696
Site_20 0.41176471 0.75000000 0.52941176 0.80952381 0.63636364 0.60000000
           Site_13    Site_14    Site_15    Site_16    Site_17    Site_18
Site_2                                                                   
Site_3                                                                   
Site_4                                                                   
Site_5                                                                   
Site_6                                                                   
Site_7                                                                   
Site_8                                                                   
Site_9                                                                   
Site_10                                                                  
Site_11                                                                  
Site_12                                                                  
Site_13                                                                  
Site_14 0.33333333                                                       
Site_15 0.57894737 0.80000000                                            
Site_16 0.55555556 0.78947368 0.05882353                                 
Site_17 0.22222222 0.36842105 0.52941176 0.50000000                      
Site_18 0.54545455 0.73913043 0.14285714 0.20000000 0.50000000           
Site_19 0.73913043 0.83333333 0.27272727 0.33333333 0.61904762 0.28000000
Site_20 0.60000000 0.80952381 0.26315789 0.22222222 0.55555556 0.09090909
           Site_19
Site_2            
Site_3            
Site_4            
Site_5            
Site_6            
Site_7            
Site_8            
Site_9            
Site_10           
Site_11           
Site_12           
Site_13           
Site_14           
Site_15           
Site_16           
Site_17           
Site_18           
Site_19           
Site_20 0.30434783

Tipos de distancias

La disimilitud entre ‘sitios’ se puede calcular de varias maneras: euclidean, manhattan, gower, canberra, bray, jaccard…

Para ello usamos el argumento method

dist <- vegdist(com, method="euclidean")
dist <- vegdist(com, method="bray")
dist <- vegdist(com, method="jaccard")
head(dist)

[1] 0.2500000 0.4285714 0.8888889 0.8888889 0.8888889 0.8750000

Clasificación jerárquica

Para ello usamos la función hclust sobre la matriz de distancias

hc <- hclust(dist)
hc


Call:
hclust(d = dist)

Cluster method   : complete 
Distance         : jaccard 
Number of objects: 20

Métodos de agrupación

Métodos para realizar la agrupación hay varios: single, complete, average, centroid…

Especificamos el método con el argumento method.

hc <- hclust(dist, method="single")
hc <- hclust(dist, method="centroid")
hc <- hclust(dist, method="average")
hc <- hclust(dist, method="complete")
hc


Call:
hclust(d = dist, method = "complete")

Cluster method   : complete 
Distance         : jaccard 
Number of objects: 20

Visualizar clasificaciones

Las clasificaciones jerárquicas se pueden visualizar como un árbol filogenético con la función plot

plot(hc, hang=-1)

Interpretación

Establecer grupos en un árbol no es siempre trivial

Se puede usar un umbral para determinar los grupos
O establecer un número determinado de grupos

Visualizar clasificaciones con un umbral

plot(hc, hang=-1) 
rect.hclust(hc, h=0.7)

Visualizar clasificaciones con número de grupos

plot(hc, hang=-1)
rect.hclust(hc, k=4)

Extraer grupos

En ocasiones es interesante extraer la asignación de cada sitio a un grupo

Para ello podemos usar la función cutree

grp <- cutree(hc, h=0.7)
grp <- cutree(hc, k=4)
grp

 Site_1  Site_2  Site_3  Site_4  Site_5  Site_6  Site_7  Site_8  Site_9 Site_10 
      1       1       1       2       2       3       2       3       4       4 
Site_11 Site_12 Site_13 Site_14 Site_15 Site_16 Site_17 Site_18 Site_19 Site_20 
      4       4       4       4       2       2       4       2       2       2

Combinar ordenación y agrupamientos

Dibujar agrupamientos sobre los gráficos de ordenación

Para ello usamos la función ordihull

plot(com_ca, display="sites")
ordihull(com_ca, grp, lty=2, col="red")

Hay más opciones…

También se pueden usar las funciones ordispider y ordiellipse

plot(com_ca, display="sites")
ordispider(com_ca, grp, lty=2, col="red")

… que elegirás en función de tu necesidad

Para ello usamos las funciones ordispider y ordiellipse

plot(com_ca, display="sites")
ordiellipse(com_ca, grp, lty=2, col="red")