Modelos Jerárquicos de Comunidades de Especies en R

Hierarchical Models of Species Communities (HMSC)

Diego Nieto Lugilde

Universidad de Córdoba (España)

2024-10-18

Cargamos algunos datos

library(xlsx)
env <- read.xlsx("data/sciberras_ambiente.xlsx", 1, row.names = 1)
com <- read.xlsx("data/sciberras_especies.xlsx", 1, row.names = 1)

Preparamos un poco los datos

comm <- as.matrix(com)

envm <- scale(env[, 4:7])
envm <- as.data.frame(envm)

sites <- env[, 1:3]

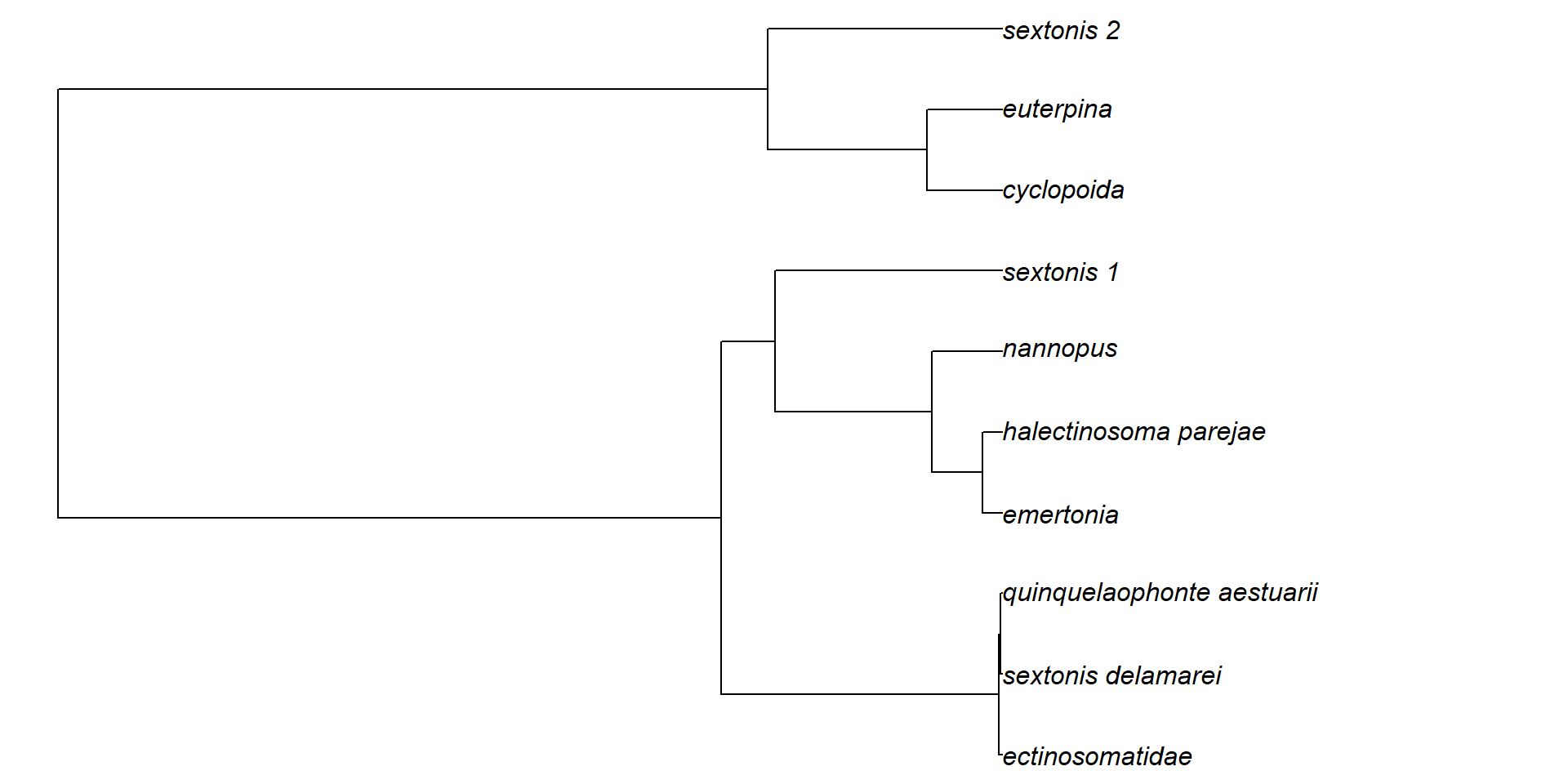
Simulamos unos datos filogenéticos

phy <- ape::rcoal(n = ncol(comm), 
                 tip.label = colnames(comm), 
                 br = "coalescent")
plot(phy, no.margin = TRUE)

Definimos el diseño experimental

library(Hmsc)
studyDesign <- data.frame(rio = as.factor(sites$rio),
                         mes = as.factor(sites$mes))
rioL <- HmscRandomLevel(units = levels(sites$rio))
mesL <- HmscRandomLevel(units = levels(sites$mes))

rioL$nfMin <- 2
mesL$nfMin <- 2

Especificamos la estructura del modelo

m0 <- Hmsc(Y = comm, 
         XData = envm, 
         XFormula = ~1,
         studyDesign = studyDesign, 
         ranLevels = list(rio = rioL, mes = mesL),
         distr = "lognormal poisson")

m1 <- Hmsc(Y = comm, 
           XData = envm,
           XFormula = ~materia_org + poly(temperatura ,degree = 2, raw = TRUE) + salinidad + ph,
           distr = "lognormal poisson")


m_env <- Hmsc(Y = comm, 
          XData = envm,
          XFormula = ~materia_org + poly(temperatura ,degree = 2, raw = TRUE)  + salinidad + ph,
          studyDesign = studyDesign, 
          ranLevels = list(rio = rioL, mes = mesL),
          distr = "lognormal poisson")

m_env_phy <- Hmsc(Y = comm,
         XData = envm, 
         XFormula = ~materia_org + poly(temperatura ,degree = 2, raw = TRUE)  + salinidad + ph,
         phyloTree = phy,
         studyDesign = studyDesign, 
         ranLevels = list(rio = rioL, mes = mesL),
         distr = "lognormal poisson")

Definimos los parámetros para las Cadenas de Markov Monte Carlo

samples <- 100 # Este valor debería ser más alto. Del orden de 100000 hacia arriba.
thin <- 1 # Este valor también suele ser más alto. Del orden de 50-100 hacia arriba.
transient <- 500*thin
nChains <- 4

Se calibran y estiman los parámetros del modelos con las MCMC

m0 <- sampleMcmc(m0, 
               thin = thin, 
               samples = samples, 
               transient = transient, 
               nChains = nChains, 
               nParallel = nChains)
m1 <- sampleMcmc(m1, 
               thin = thin, 
               samples = samples, 
               transient = transient, 
               nChains = nChains, 
               nParallel = nChains)
m_env <- sampleMcmc(m_env, 
               thin = thin, 
               samples = samples, 
               transient = transient, 
               nChains = nChains, 
               nParallel = nChains)
m_env_phy <- sampleMcmc(m_env_phy, 
               thin = thin, 
               samples = samples, 
               transient = transient, 
               nChains = nChains, 
               nParallel = nChains)

Convertimos los resultados en objetos CODA, son un tipo de datos de análisis bayesianos en R

mpost_m0 <- convertToCodaObject(m0)
mpost_m1 <- convertToCodaObject(m1)
mpost_m_env <- convertToCodaObject(m_env)
mpost_m_env_phy <- convertToCodaObject(m_env_phy)

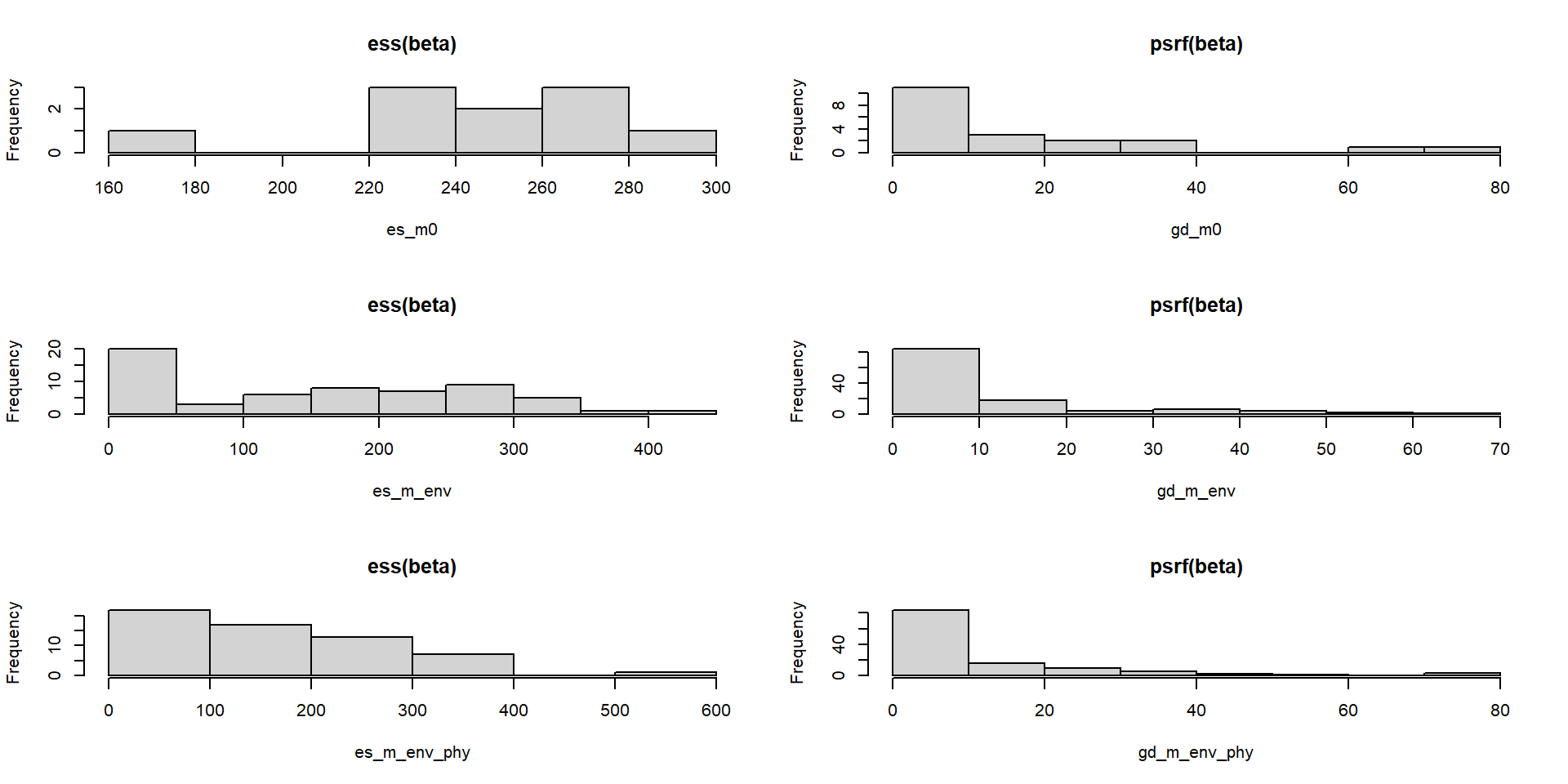
Calculamos dos estadísticos de calibración de MCMC

es_m0 <- effectiveSize(mpost_m0$Beta)
es_m1 <- effectiveSize(mpost_m1$Beta)
es_m_env <- effectiveSize(mpost_m_env$Beta)
es_m_env_phy <- effectiveSize(mpost_m_env_phy$Beta)
gd_m0 <- gelman.diag(mpost_m0$Beta, multivariate=FALSE)$psrf
gd_m_env <- gelman.diag(mpost_m_env$Beta, multivariate=FALSE)$psrf
gd_m_env_phy <- gelman.diag(mpost_m_env_phy$Beta, multivariate=FALSE)$psrf

Dibujamos las gráficas de esos dos parámetros

Effective size debería estar entorno al número de muestras de las MCMC (samples * nChains). El diagnóstico de Gelman debería estar entorno a 1.

par(mfrow=c(3,2))
hist(es_m0, main="ess(beta)")
hist(gd_m0, main="psrf(beta)")
hist(es_m_env, main="ess(beta)")
hist(gd_m_env, main="psrf(beta)")
hist(es_m_env_phy, main="ess(beta)")
hist(gd_m_env_phy, main="psrf(beta)")

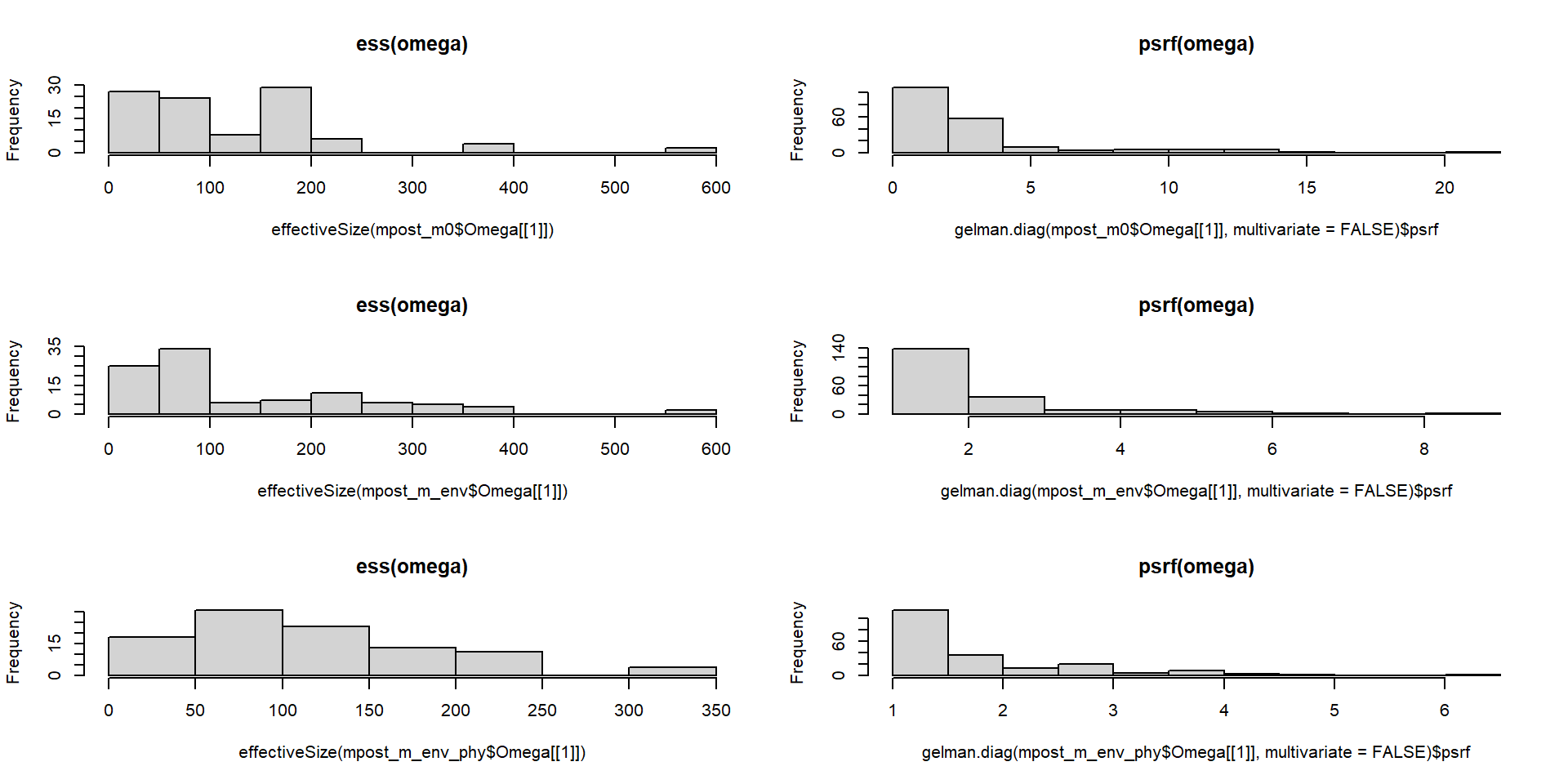
… lo mismo pero con los valores de Omega, que son los coeficientes de interacciones entre especies

par(mfrow=c(3,2))
hist(effectiveSize(mpost_m0$Omega[[1]]), main="ess(omega)")
hist(gelman.diag(mpost_m0$Omega[[1]], multivariate=FALSE)$psrf, main="psrf(omega)")
hist(effectiveSize(mpost_m_env$Omega[[1]]), main="ess(omega)")
hist(gelman.diag(mpost_m_env$Omega[[1]], multivariate=FALSE)$psrf, main="psrf(omega)")
hist(effectiveSize(mpost_m_env_phy$Omega[[1]]), main="ess(omega)")
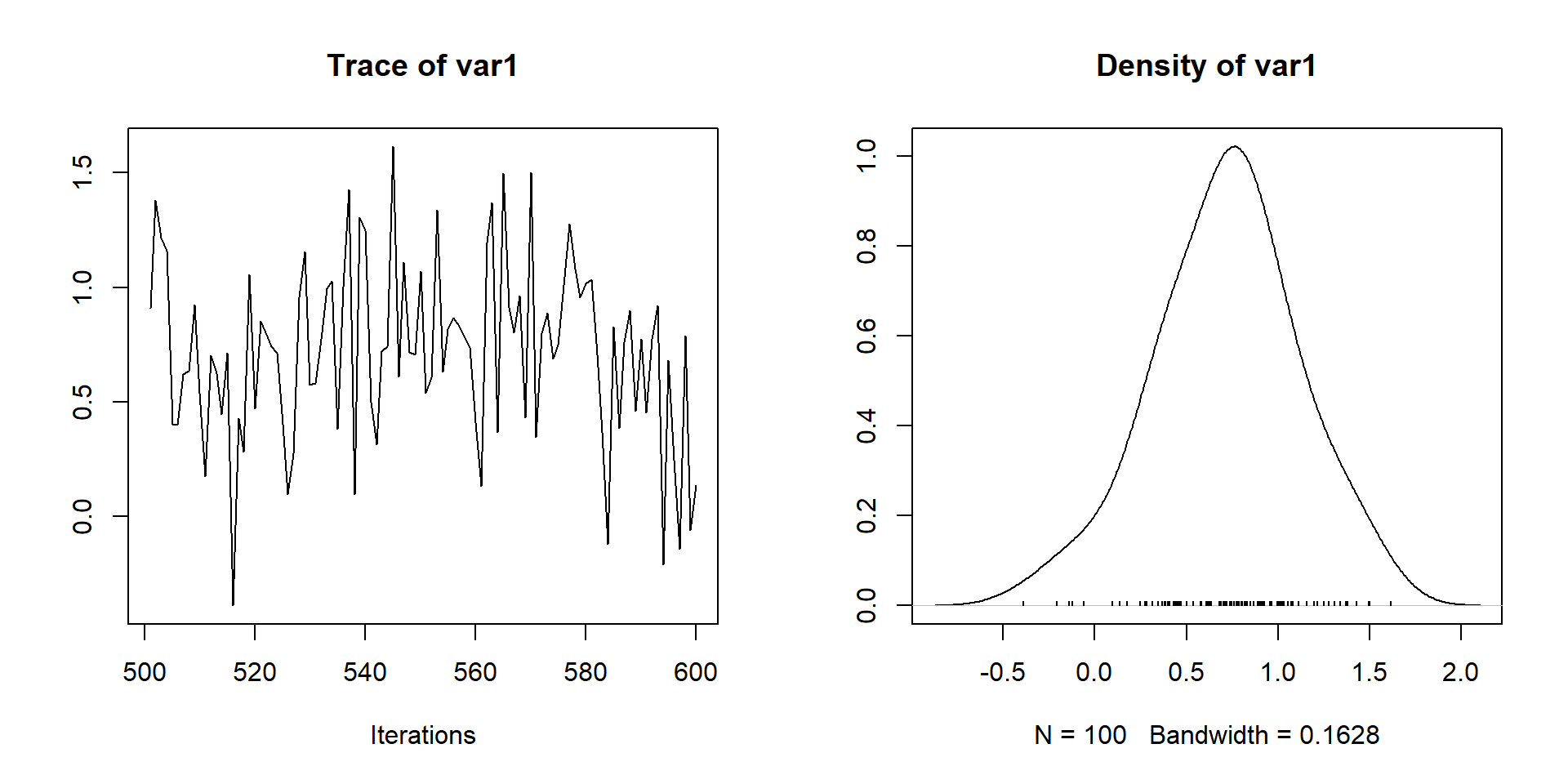
hist(gelman.diag(mpost_m_env_phy$Omega[[1]], multivariate=FALSE)$psrf, main="psrf(omega)")

Tambien podemos dibujar algunas de las cadenas para visulizar su forma y ver si se han estabilizado

plot(mpost_m0$Beta[[1]][,2])

Para evaluar el modelo en términos de la distribución/abundancia de las especies, debemos hacer predicciones primero.

preds_m0 <- computePredictedValues(m0)
evaluateModelFit(hM = m0, predY = preds_m0)
$RMSE
 [1] 178.7046818 112.1060668  20.0050140  25.8061127   1.4742253   1.2257749
 [7]   0.3629371   0.5948718   0.4136221   0.7108976

$SR2
 [1]  0.44104705  0.43882516  0.14058017  0.33967948  0.00404370  0.12155108
 [7] -0.01259728  0.05565401  0.03797939  0.06015246

$O.AUC
 [1] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5

$O.TjurR2
 [1] 0 0 0 0 0 0 0 0 0 0

$O.RMSE
 [1] 0.5814019 0.5566499 0.8960005 0.8049145 0.9115843 0.9786452 0.9858149
 [8] 0.9786452 0.9786452 0.9858149

$C.SR2
 [1] 0.3439112993 0.3598536094 0.0257322387 0.1150386032 0.0001164009
 [6]           NA           NA           NA           NA           NA

$C.RMSE
 [1] 217.0444042 134.5360937  44.7811536  42.4439580   3.4896220   5.6977254
 [7]   0.6537211   0.3809210   0.5918066   0.2427098
preds_m1 <- computePredictedValues(m1)
evaluateModelFit(hM = m1, predY = preds_m1)
$RMSE
 [1] 239.5894479 124.3036980  19.9331009  28.0490736   1.4336509   1.2093620
 [7]   0.2752305   0.3071712   0.3476443   0.2666874

$SR2
 [1]  0.2094872098  0.2722988542  0.0342582931  0.1587915733 -0.0036198349
 [6]  0.0643153798  0.0001552795 -0.0078898226  0.0215802988  0.0038819876

$O.AUC
 [1] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5

$O.TjurR2
 [1] 0 0 0 0 0 0 0 0 0 0

$O.RMSE
 [1] 0.5814019 0.5566499 0.8960005 0.8049145 0.9115843 0.9786452 0.9858149
 [8] 0.9786452 0.9786452 0.9858149

$C.SR2
 [1] 0.16373436 0.14570572 0.07679719 0.04803554 0.27188927 0.25000000
 [7]         NA         NA         NA         NA

$C.RMSE
 [1] 287.3041422 146.8263550  43.3889397  39.8621564   3.3175464   5.7124472
 [7]   0.8489667   0.8425653   0.6761803   0.7612070
preds_m_env <- computePredictedValues(m_env)
evaluateModelFit(hM = m_env, predY = preds_m_env)
$RMSE
 [1] 198.0809861 121.5655796  19.7023785  25.8081348   1.4474939   1.1704319
 [7]   0.3259737   0.2917941   0.2623690   0.2711962

$SR2
 [1]  0.3113252526  0.4452635687  0.0845909888  0.2838581631 -0.0005258901
 [6]  0.0908541598 -0.0008454106  0.0042133520  0.0280228758  0.0033816425

$O.AUC
 [1] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5

$O.TjurR2
 [1] 0 0 0 0 0 0 0 0 0 0

$O.RMSE
 [1] 0.5814019 0.5566499 0.8960005 0.8049145 0.9115843 0.9786452 0.9858149
 [8] 0.9786452 0.9786452 0.9858149

$C.SR2
 [1] 0.24034333 0.27846395 0.07058145 0.12653319 0.26079293 1.00000000
 [7]         NA         NA         NA         NA

$C.RMSE
 [1] 242.4261169 145.5229074  43.8888197  40.7282525   3.4359286   5.5406217
 [7]   0.7611457   0.8769854   0.7229513   0.7906554
preds_m_env_phy <- computePredictedValues(m_env_phy)
evaluateModelFit(hM = m_env_phy, predY = preds_m_env_phy)
$RMSE
 [1] 216.0099471 121.4572935  19.4606626  25.7175698   1.4555382   1.2045312
 [7]   0.2779336   0.4405696   0.7282538   0.2475604

$SR2
 [1]  3.682232e-01  4.713293e-01  1.199537e-01  3.359516e-01  2.578516e-02
 [6]  9.073820e-02 -1.552795e-04  2.689076e-02  1.685341e-02  6.901311e-05

$O.AUC
 [1] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5

$O.TjurR2
 [1] 0 0 0 0 0 0 0 0 0 0

$O.RMSE
 [1] 0.5814019 0.5566499 0.8960005 0.8049145 0.9115843 0.9786452 0.9858149
 [8] 0.9786452 0.9786452 0.9858149

$C.SR2
 [1] 0.25446799 0.30267563 0.17566157 0.07310235 0.16254407 1.00000000
 [7]         NA         NA         NA         NA

$C.RMSE
 [1] 264.5851587 145.7033563  43.2717989  41.7909492   3.4773240   5.6963881
 [7]   0.7905187   0.6136172   0.4047374   0.7921033

También es posible realizar evaluación por validación cruzada

partition_env <- createPartition(m_env, nfolds = 4)
preds_m_env = computePredictedValues(m_env, 
                               partition = partition_env,
                               nParallel = nChains)
Cross-validation, fold 1 out of 4
Cross-validation, fold 2 out of 4
Cross-validation, fold 3 out of 4
Cross-validation, fold 4 out of 4
evaluateModelFit(hM = m_env, predY = preds_m_env)
$RMSE
 [1] 228.5461386 166.9150113  20.1004411  28.3106774   1.4873049   1.2555333
 [7]   0.2856651   0.3612464   0.3271817   0.2471069

$SR2
 [1]  1.205130e-01  2.006534e-01  1.955293e-02  4.666595e-02 -1.003100e-02
 [6]  1.305100e-03  6.901311e-05 -2.987862e-03  1.512605e-02 -5.590062e-03

$O.AUC
 [1] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5

$O.TjurR2
 [1] 0 0 0 0 0 0 0 0 0 0

$O.RMSE
 [1] 0.5814019 0.5566499 0.8960005 0.8049145 0.9115843 0.9786452 0.9858149
 [8] 0.9786452 0.9786452 0.9858149

$C.SR2
 [1]  0.074497388  0.096339360  0.004112355  0.001445167 -0.008351153
 [6] -0.250000000           NA           NA           NA           NA

$C.RMSE
 [1] 278.9709740 198.4772048  44.9055812  43.1712286   3.5037181   5.8779952
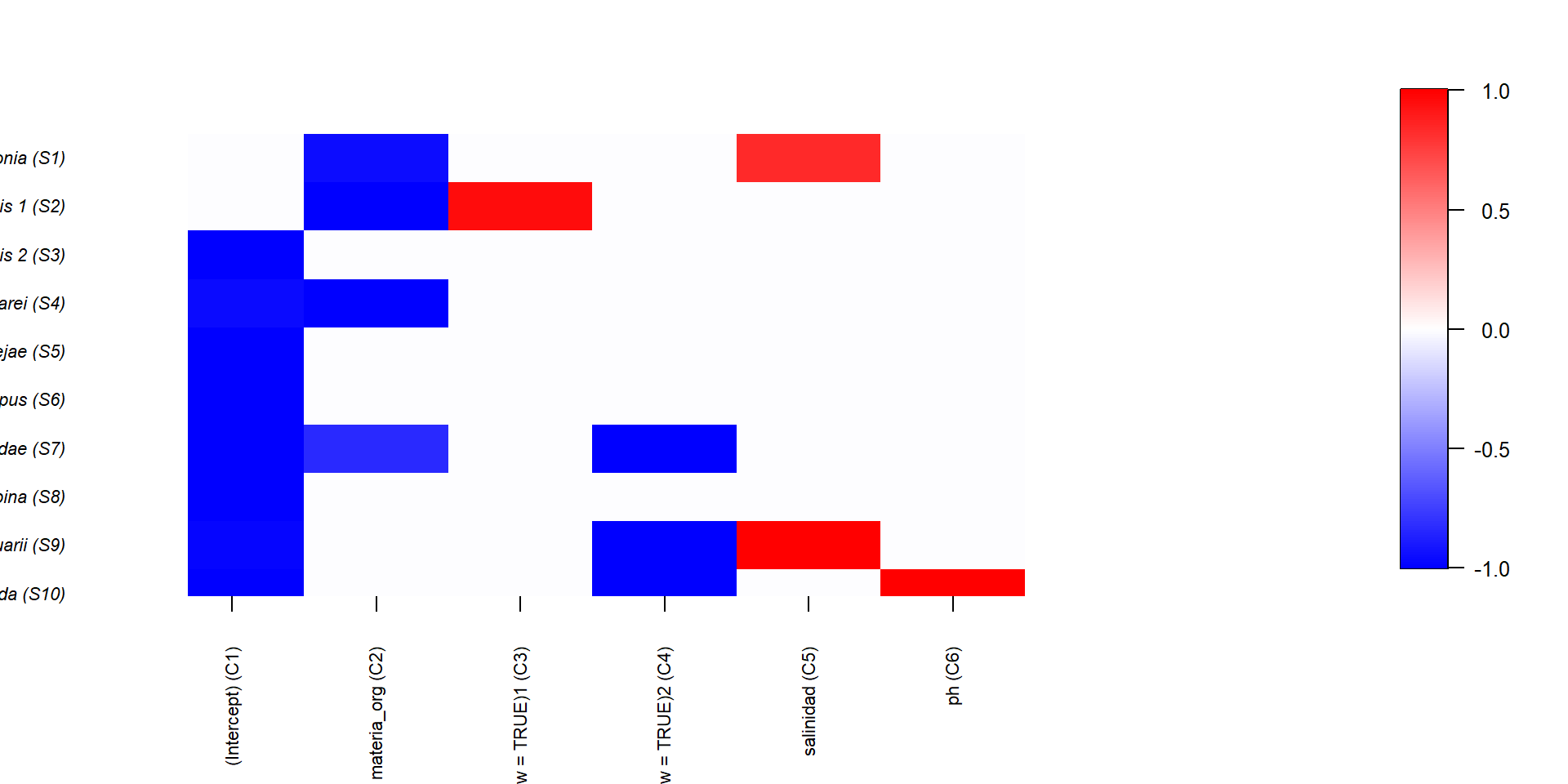
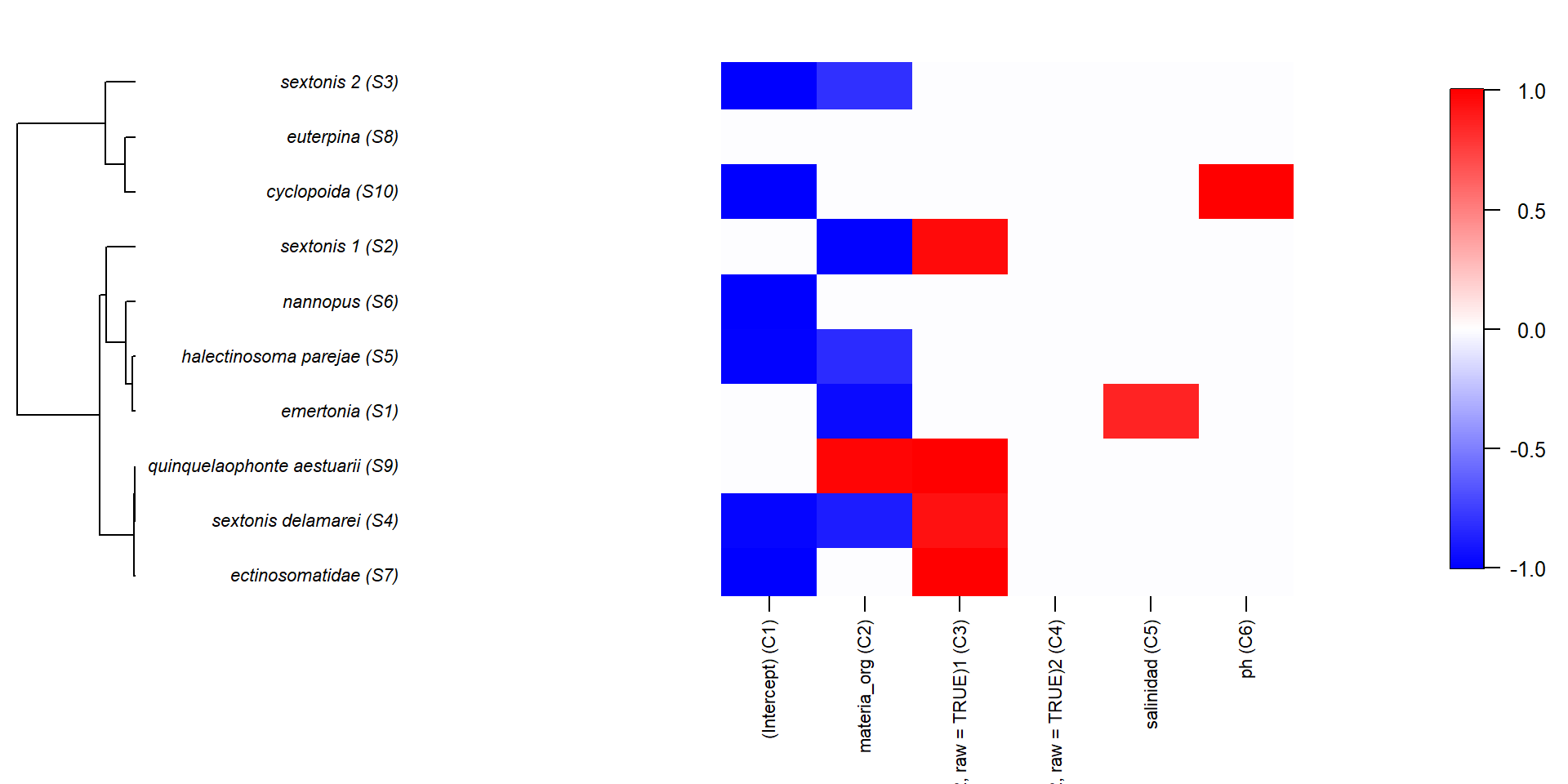
 [7]   0.8099910   0.8245285   0.6666862   0.8732730

Una vez que tengamos un modelo sólido. Nos interesa ver que papel juegan las variables ambientales en las especies/comunidades.

postBeta <- getPostEstimate(m_env, parName = "Beta")
plotBeta(m_env, 
         post = postBeta, 
         param = "Support", 
         supportLevel = 0.9)

También podemos ver su relación con la información filogenética, si la hemos incluido en el modelo

postBeta <- getPostEstimate(m_env_phy, parName = "Beta")
plotBeta(m_env_phy, 
         post = postBeta, 
         param = "Support", 
         supportLevel = 0.9,
         plotTree = TRUE)
[1] 0.3 1.0 0.0 1.0

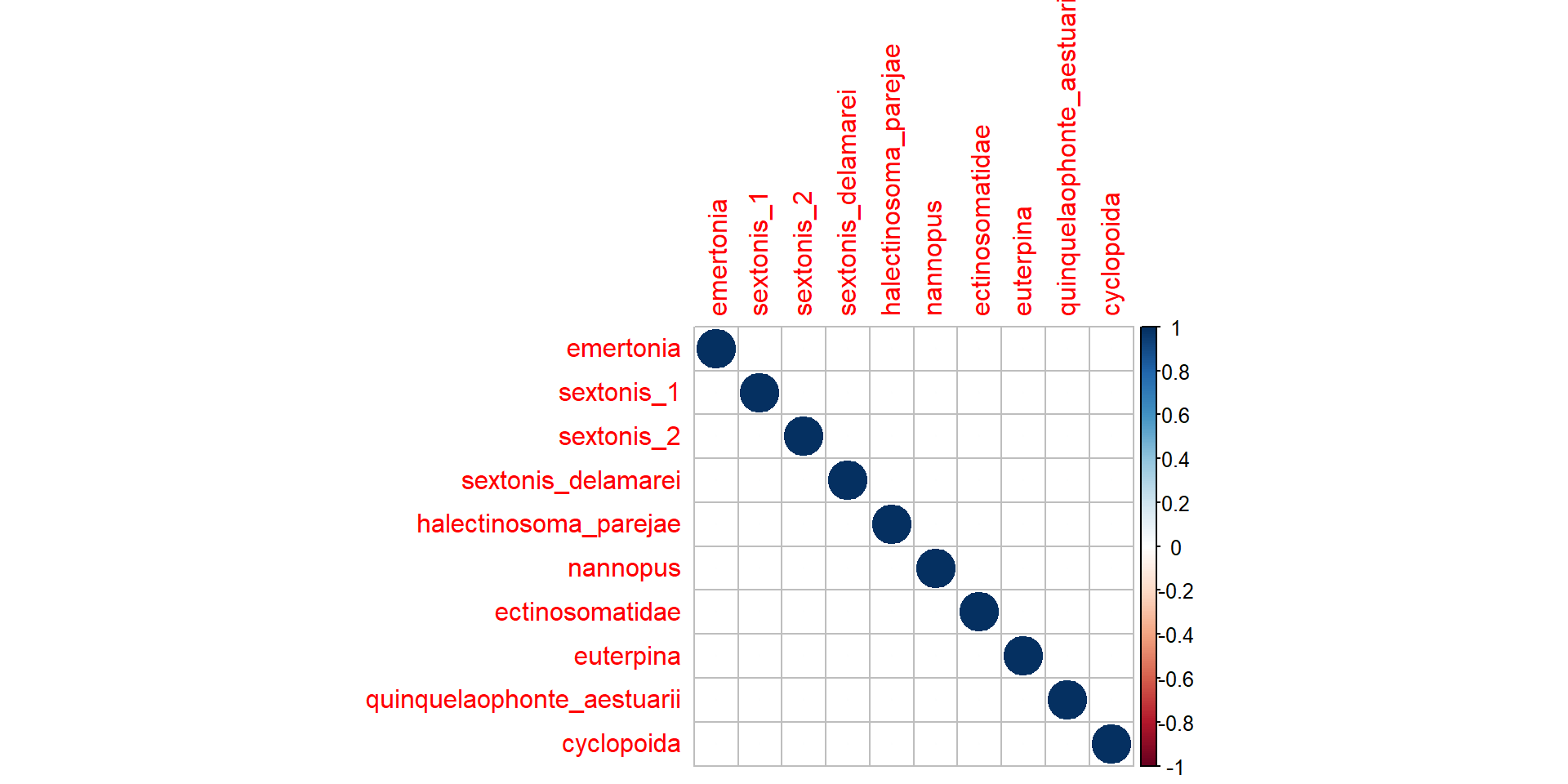
Otro aspecto importante/novedoso es estimar las correlaciones entre especies

library(corrplot)
OmegaCor <- computeAssociations(m_env)
supportLevel <- 0.95
toPlot <- ((OmegaCor[[1]]$support > supportLevel) +
           (OmegaCor[[1]]$support < (1-supportLevel)
            ) > 0) * OmegaCor[[1]]$mean
corrplot(toPlot)

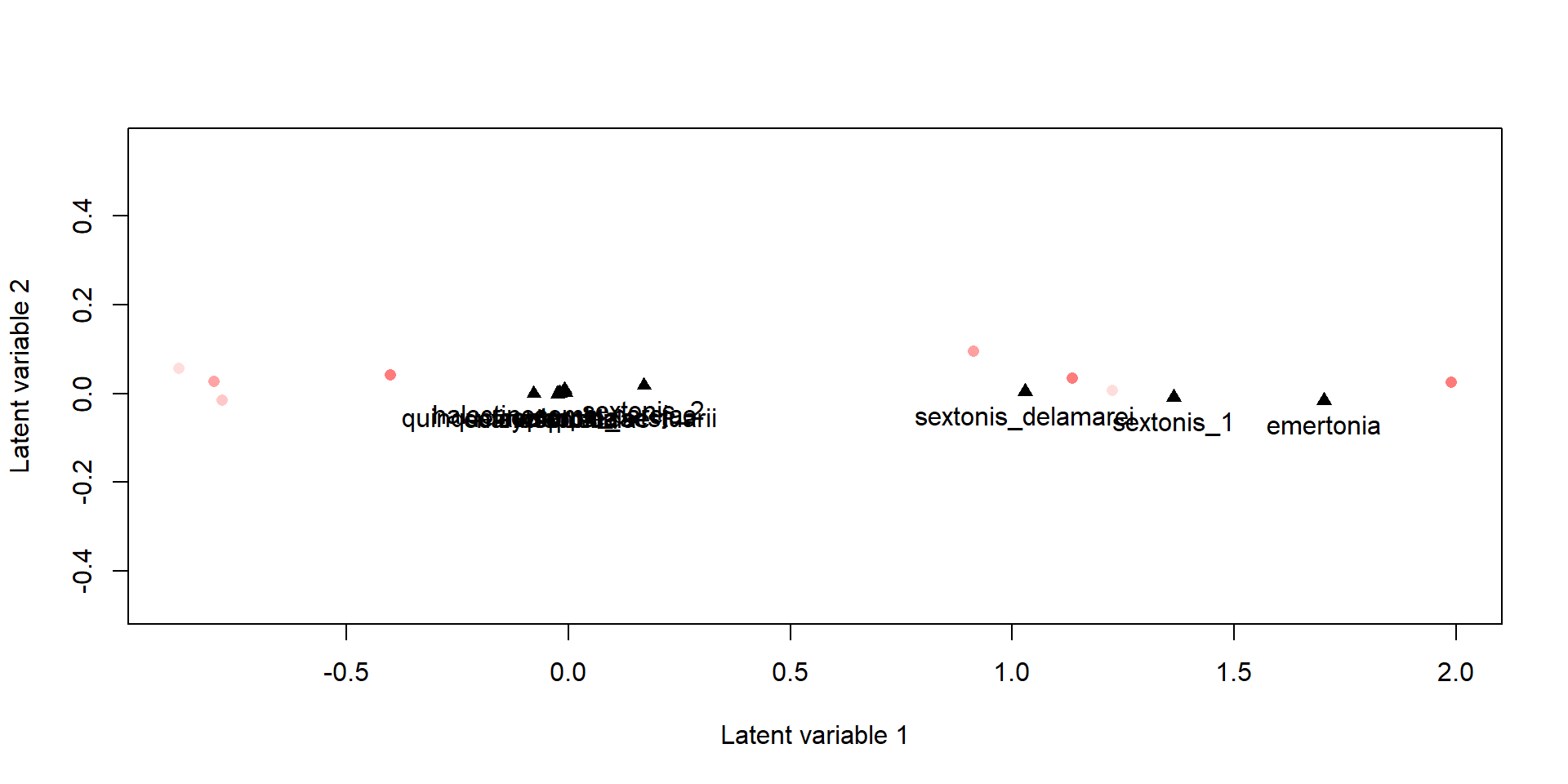
Cuando especificamos un modelo sin variables ambientales, estamos haciendo un modelo “unconstrained” o indirecto. Por lo que se puede usar para generar gráficos de ordenación.

etaPost <- getPostEstimate(m0, "Eta")
lambdaPost <- getPostEstimate(m0, "Lambda")
biPlot(m0, 
       etaPost = etaPost, 
       lambdaPost = lambdaPost, 
       factors = c(1,2), 
       "ph")

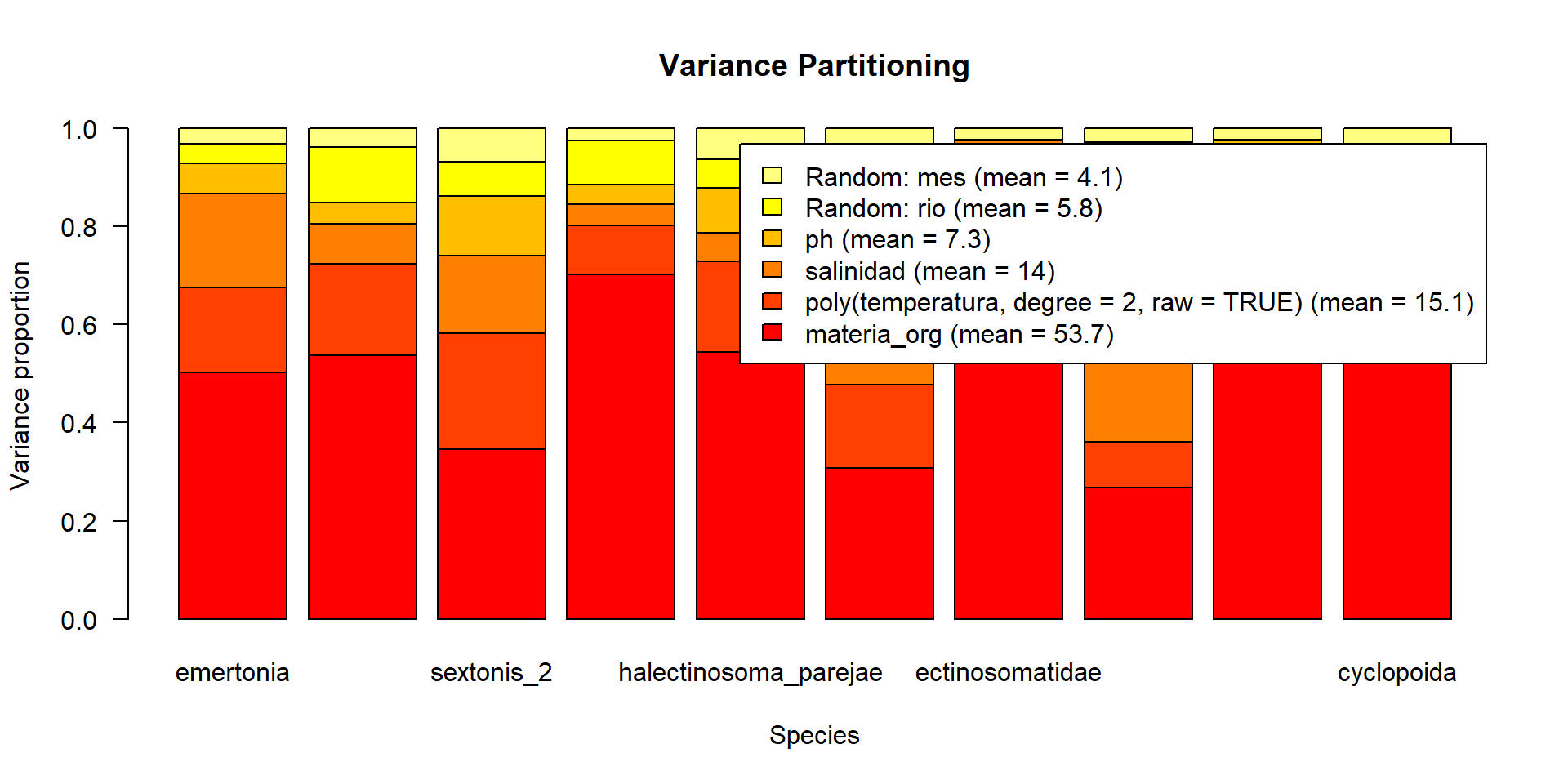
En este tipo de modelos, la importancia de cada variable se mide en términos de variación explicada y se calcula con análisis de particionado de la varianza

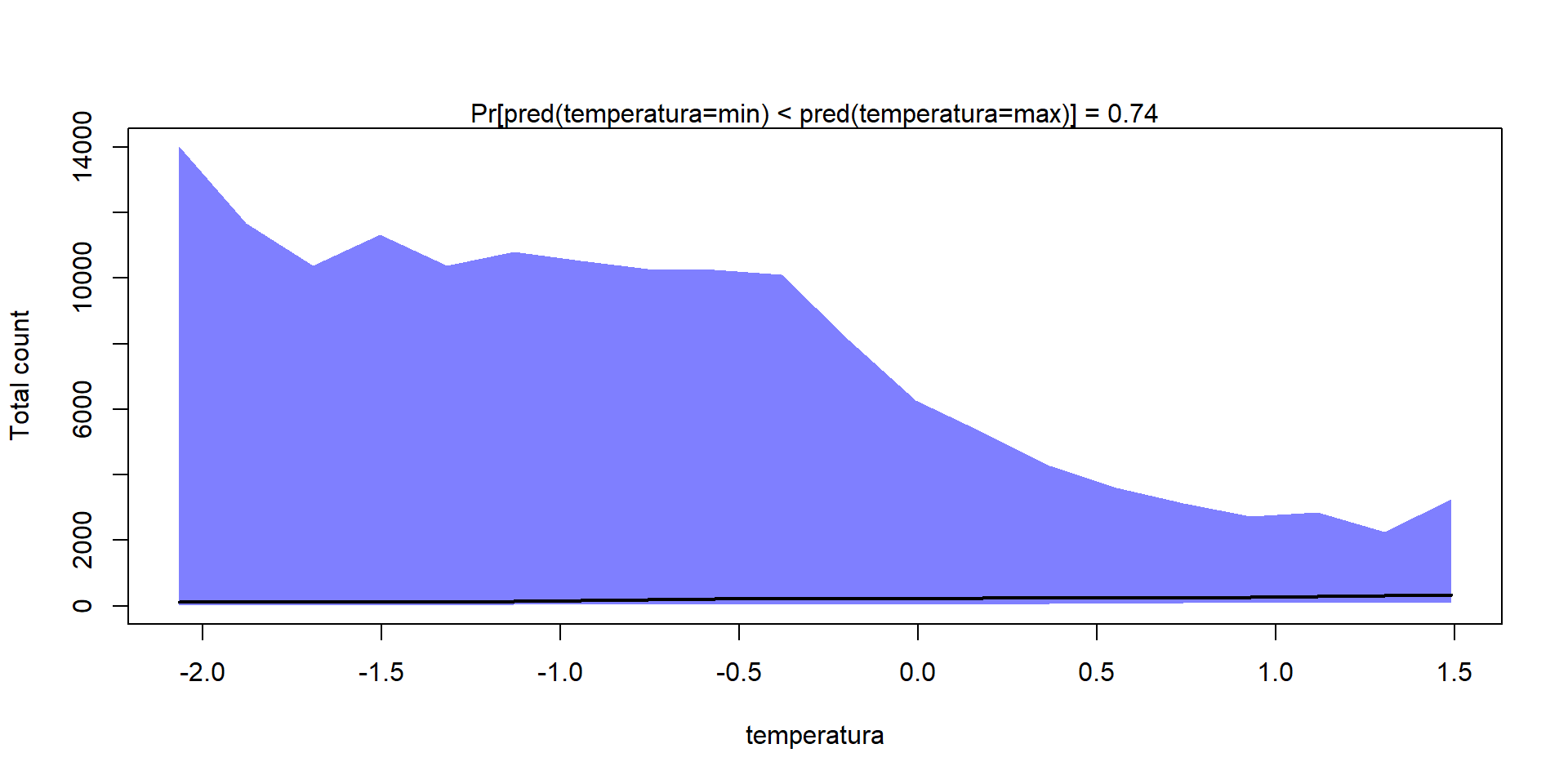
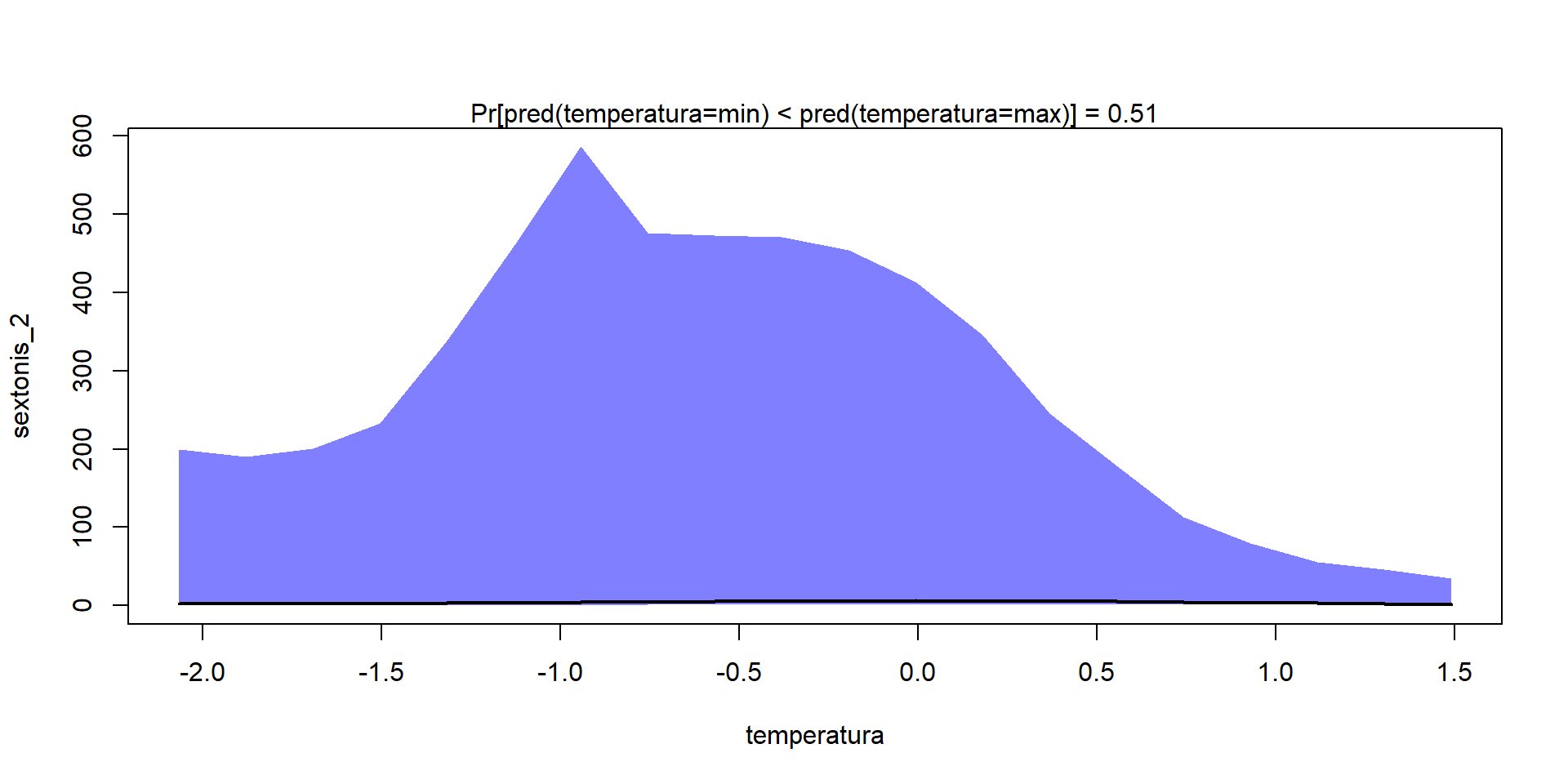
VP = computeVariancePartitioning(m_env)
plotVariancePartitioning(m_env, VP = VP)

Como en los Modelos de Distribución de Especies, podemos calcular curvas de respuesta de cada especie/comunidad a las variables ambientales

Gradient = constructGradient(m1, focalVariable = "temperatura",
non.focalVariables = list("habitat"=list(3,"open")))
Gradient$XDataNew
    temperatura   materia_org    salinidad          ph
1  -2.065315281 -0.1667234554 -0.501380262  0.37285247
2  -1.878146837 -0.1516142030 -0.455942859  0.33906285
3  -1.690978393 -0.1365049507 -0.410505456  0.30527323
4  -1.503809949 -0.1213956984 -0.365068052  0.27148361
5  -1.316641505 -0.1062864460 -0.319630649  0.23769400
6  -1.129473060 -0.0911771937 -0.274193245  0.20390438
7  -0.942304616 -0.0760679413 -0.228755842  0.17011476
8  -0.755136172 -0.0609586890 -0.183318438  0.13632514
9  -0.567967728 -0.0458494366 -0.137881035  0.10253552
10 -0.380799284 -0.0307401843 -0.092443632  0.06874590
11 -0.193630840 -0.0156309320 -0.047006228  0.03495628
12 -0.006462395 -0.0005216796 -0.001568825  0.00116666
13  0.180706049  0.0145875727  0.043868579 -0.03262296
14  0.367874493  0.0296968251  0.089305982 -0.06641258
15  0.555042937  0.0448060774  0.134743386 -0.10020220
16  0.742211381  0.0599153298  0.180180789 -0.13399182
17  0.929379825  0.0750245821  0.225618193 -0.16778144
18  1.116548270  0.0901338344  0.271055596 -0.20157106
19  1.303716714  0.1052430868  0.316492999 -0.23536068
20  1.490885158  0.1203523391  0.361930403 -0.26915030
predY <- predict(m1, 
                XData=Gradient$XDataNew, 
                studyDesign=Gradient$studyDesignNew,
                ranLevels=Gradient$rLNew, 
                expected=TRUE)
plotGradient(m1, Gradient, pred=predY, measure="S")

[1] 0.74
plotGradient(m1, Gradient, pred=predY, measure="Y", index = 3)

[1] 0.5125

AEMeR