# Ejercicio 1.
# Parte 1
seq(1, 40, by = 2)
# Parte 2
seq(1, 40, by = -2)
# Este código da error porque especifiqué algo mal :)Análisis espaciales y multivariantes con R (AEMeR) aplicados a estudios de biodiversidad
Ejercicios de análisis multivariante
Los ejercicios tendréis que entregarlos para la evaluación del curso. Para ello, crea un script de R con RStudio. Ponle el nombre ejercicios_t3_[nombre]_[apellido].R. Dicho script deberá estar organizado con comentarios en castellano (poniendo una almohadilla # delante) y justo detrás el código necesario para realizar el ejercicio (ver ejemplo debajo). Además, si el ejercicio pide reflexionar sobre el resultado use los comentarios (con la #) para indicar sus reflexiones debajo del código. Una vez los tengáis completos podéis mandármelos por email.
Parte 1. Análisis de ordenación
1. Carga los datos que os he dejado en la página web (muchas gracias Michelle :). Se trata de dos tablas de excel. Una con variables abióticas (ambiente) y otra de variables bióticas (especies) tomados en las zonas de desembocaduras de varios ríos entre Bahía Blanca y Mar de Plata. A la primera llámala env y a la segunda llámala com.
He modificado los datos originales de Michelle en varios sentidos. Por un lado, he rellenado/inventado varios datos de las variables ambientales que no se habían podido medir. Por otro lado, había varios puntos de muestreo que no presentaban ningún individuo de las especies estudiadas. En estos casos, he seleccionado una especie al azar y le he añadido un individuo. Ninguna de las dos cosas es correcta, pero los análisis de ordenación no aceptan puntos sin observación alguna, ni datos ausentes. Lo he hecho intencionadamente para que los datos de Michelle no estén en bruto y podamos realizar los ejercicios sin preocuparnos de los datos NA o sin observaciones.
Aquí vas a necesitar la función read.xlsx, además, deberás especificar el argumento row.names = 1 para asegurarte que lee correctamente los nombres de las filas y los carga como tales. Así no te tendrás que preocupar de eliminar la columna 1 con los nombres de los sitios de muestreo.
library(xlsx)
env <- read.xlsx("data/sciberras_ambiente.xlsx", 1, row.names = 1)
com <- read.xlsx("data/sciberras_especies.xlsx", 1, row.names = 1)2. Vamos a preparar un poco los datos. Los datos de comunidades son abundancias, por lo que tienen una distribución muy sesgada hacia la izquierda (muchos valores próximos a cero). En estos casos, es frecuente aplicar una transformación para reducir dicho sesgo. Utiliza la función log1p() sobre la matriz com. El resultado puedes llamarlo comm. Además, la tabla (data frame) env tiene varias columnas y sólo 3 de ellas son variables ambientales. Las otras dos son información que caracteriza el punto de muestreo (información del río, mes de muestreo y ubicación con respecto a la desembocadura: 100 metros al norte, 100 metros al sur, o en la misma desembocadura). Partiendo de este data frame, genera dos data frame distintos; uno llamado sites que tenga la información de caracterización del punto de muestreo (río, sitio y mes) y otro llamado envm con los datos de las variables ambientales medidas (materia_org, temperatura, salinidad y ph).
Aquí deberás usar los corchetes ([]), tal y como hemos aprendido en días anteriores.
comm <- log1p(com)
sites <- env[, 1:3]
envm <- scale(env[, 4:7])3. Como hemos comentado en clase, una primera aproximación puede ser realizar un análisis DCA para saber si en nuestros datos dominan las respuestas lineares o unimodales. Ejecuta un DCA sobre los datos transformados de las comunidades (comm) y explica que tipo de análisis realizarás a continuación y justifica por qué.
Recuerda que el análisis DCA se hace con una función del paquete vegan llamada decorana. Una vez realizado el análisis, indica si optas por un análisis linear (PCA) o unimodal (CA). Para ello, comprueba el Axis lengths del primer eje (DCA1) del DCA para ver si presenta un valor inferior a 3 o superior a 4.
library(vegan)
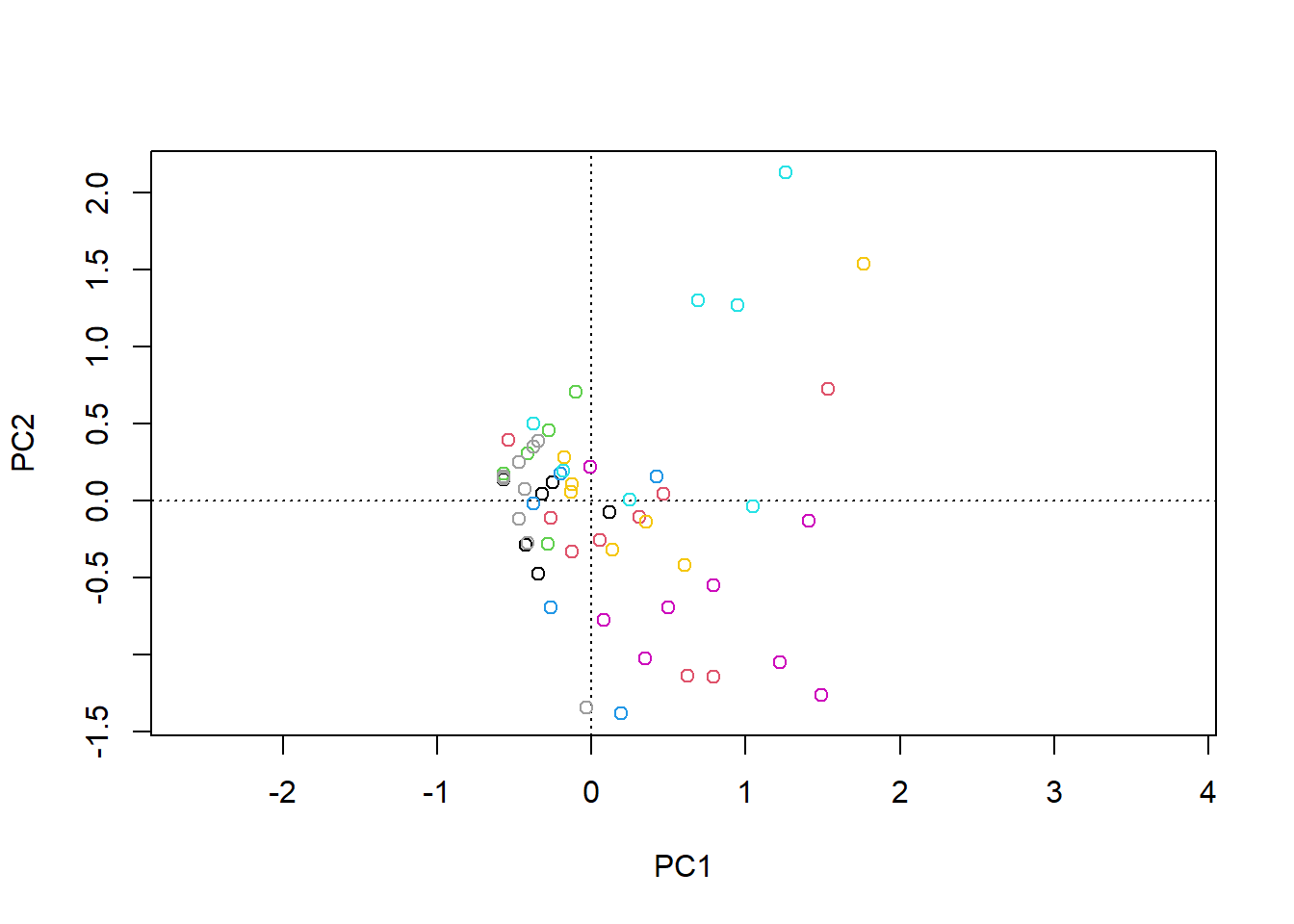
decorana(comm)4. Realiza el análisis unconstrained que hayas seleccionado en el ejercicio anterior. Guarda el resultado de dicho análisis en un objeto (ponle el nombre que quieras) y dibuja el gráfico de ordenación correspondiente. Asegúrate que el gráfico representa los puntos de los sitio con un color para cada río que se ha muestrado.
Los gráficos de ordenación se pueden realizar con la función plot() o, alternativamente, con la función ordiplot(). La función ordiplot() admite varios argumentos. Uno de ellos es display, que permite representar "sites", "species" o c("sites", "species"). Otro argumento es type = "n", que permite controlar si los elementos del gráfico se representan con "points", "text" o "none". Sin embargo, no acepta el argumento col. Por ello, para dibujar los puntos de diferentes colores deberás especificar type = "n" y luego usar la función points() para dibujar los puntos con un color diferente en cada río.
5. Ahora, realiza un análisis constrained del conjunto de datos comm, incorporando el objeto envm al análisis. Consulta la inercia total, y la proporción explicada por la parte constrained y unconstrained. Finalmente, dibuja el gráfico de ordenación resultante. ¿Qué variables explican el eje principal de variación en cuanto a composición?
Para calibrar el modelo constrained, basta con incorporar un segundo argumento a las funciones rda() y cca() con el data frame de variables ambientales.
comm_envm_rda <- rda(comm, envm)
comm_envm_rda
ordiplot(comm_envm_rda)Parte 2. Análisis de clasificación
6. Calcula la matriz de disimilitud, usando la métrica de “Bray Curtis”.
Aquí deberás usar la función vegdist sobre el objeto de comunidades original (no el transformado).
dis <- vegdist(com)7. Realiza un análisis clúster en base a la matriz de diferencias que se generó en el ejercicio anterior. Para ello, modifica el argumento method para que realice la agrupación con diferentes algoritmos.
Para realizar el análisis necesitas la función hclust(). Los valores del argumento method los puedes consultar en su ayuda (?hclust).
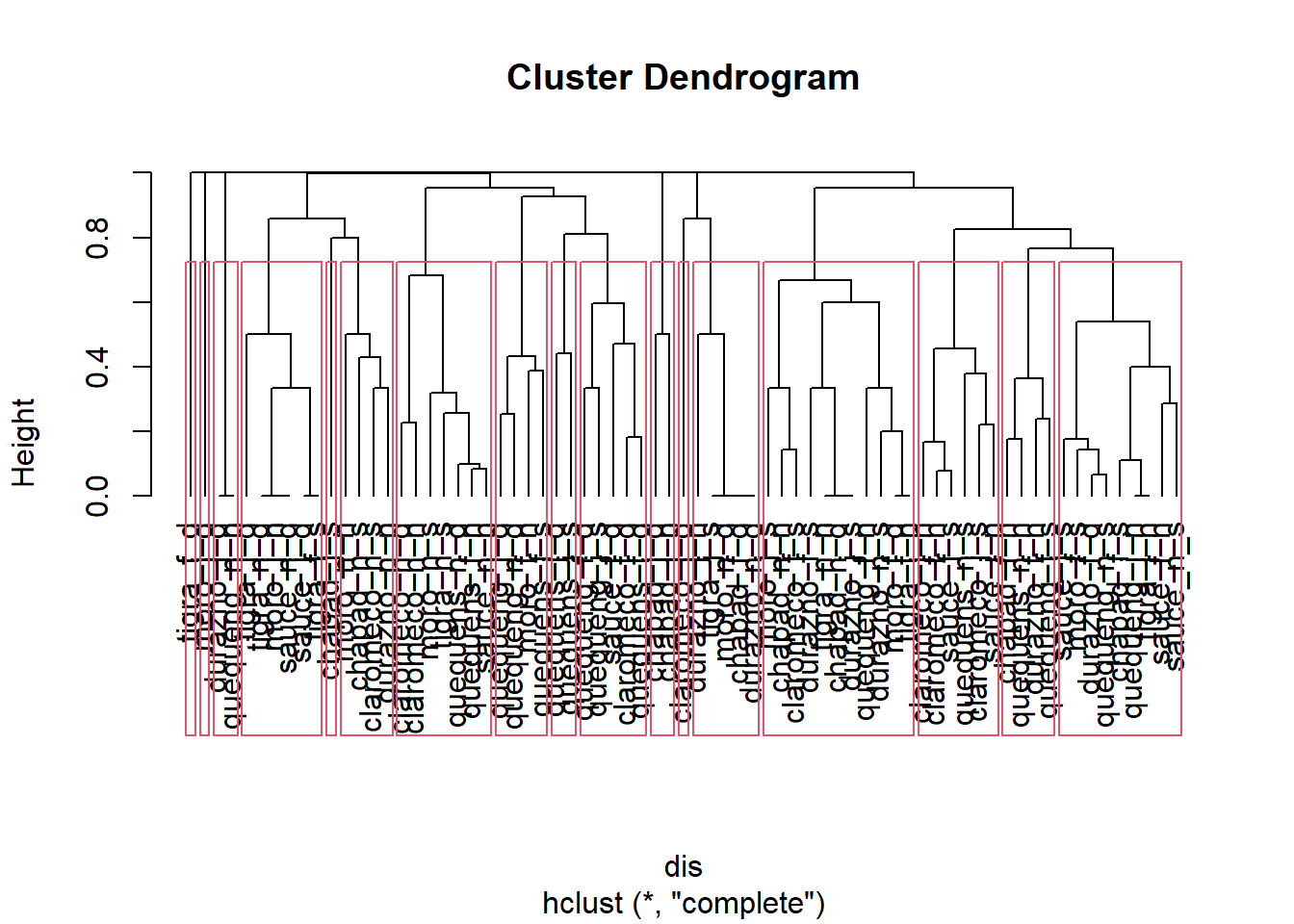
com_hc <- hclust(dis, method = "complete")8. Grafica el análisis clúster y usa el argumento hang = -1 para que dibuje el gráfico de manera más amigable. Posteriormente, añade una serie de rectángulos en el gráfico agrupando los puntos de muestreo que son similares entre si. Usa un valor de umbral o un número preestablecido de grupos (a tu elección)
Aquí puedes usar la función rect.hclust. En esta función podrás usar un valor de umbral (h = xxx) o un número preestablecido de grupos (n = xxx).
9. Usando el mismo criterio que en el ejercicio anterior, genera un vector con el grupo resultante de cada sitio.
Aquí deberás usar la función cutree(), especificando los grupos con el mismo argumento que en el ejercicio anterior.
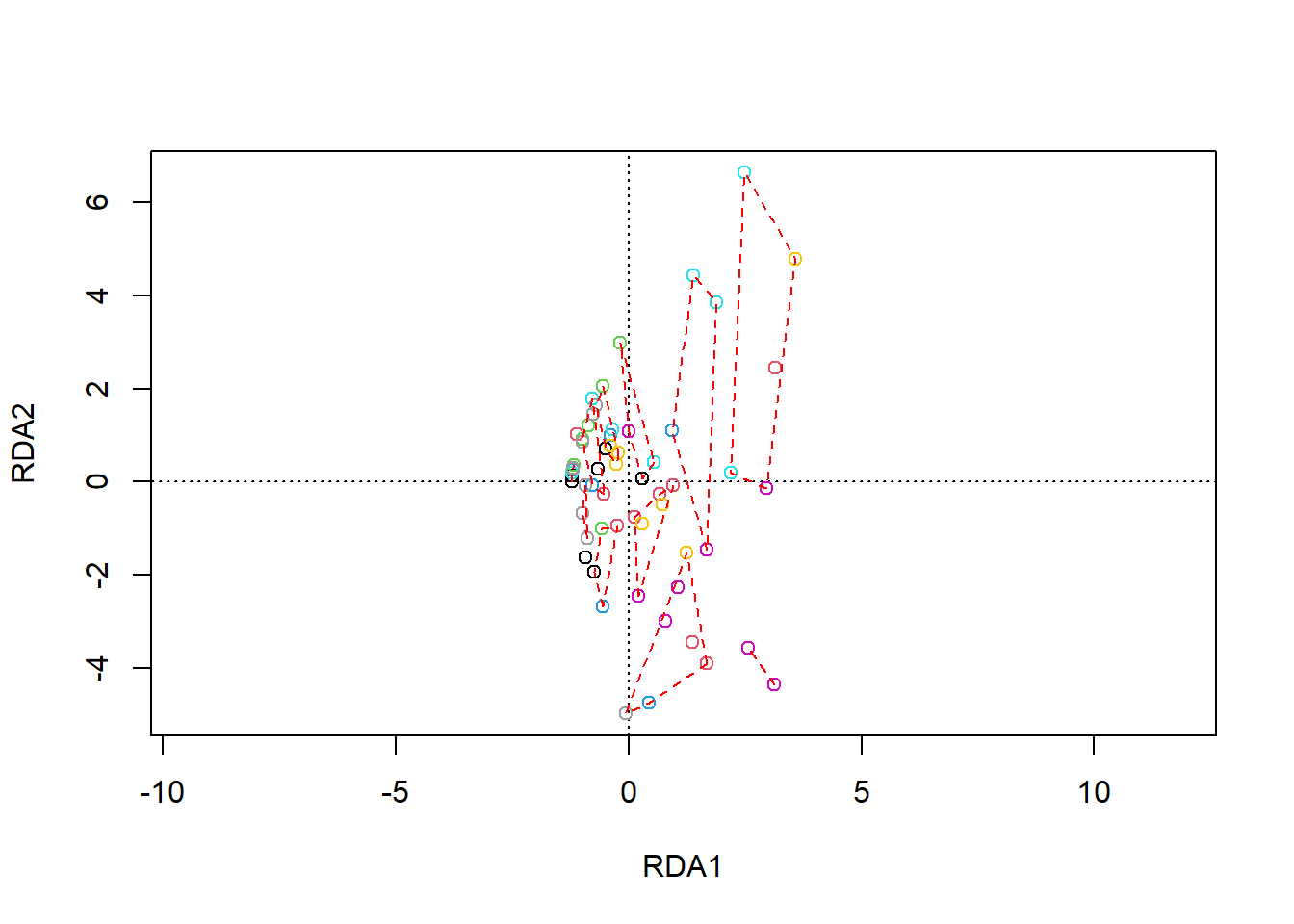
grp <- cutree(com_hc, h=0.7)10. Por último, genera de nuevo el gráfico del resultado del análisis constrained RDA. Dibuja el biplot del análisis e incorpora la información de los grupos identificados con el análisis de clasificación.
Para ello deberás dibujar el gráfico con la función ordiplot, points y ordihull, a la cual se especifica el objeto RDA y la matríz de grupos identificados previamente.